| 比赛场次 | 555 |
|---|---|
| 比赛名称 | 2022级DP专题练习赛5 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2023-02-22 18:30:00 |
| 结束时间 | 2023-02-22 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 |
| 题目名称 | 奥运物流 |
|---|---|
| 输入输出 | trans.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【问题描述】
2008 北京奥运会前夕,举国上下都在为这一盛事做好准备。为了高效率、成功地举办奥运会,对物流系统进行规划是必不可少的。
物流系统由若干物流基站组成,以 $1 \sim N$ 进行编号。每个物流基站 $i$ 都有且仅有一个后继基站 $S_i$,而可以有多个前驱基站。基站 $i$ 中需要继续运输的物资都将被运往后继基站 $S_i$,显然一个物流基站的后继基站不能是其本身。编号为 $1$ 的物流基站称为控制基站,从任何物流基站都可将物资运往控制基站。注意控制基站也有后继基站,以便在需要时进行物资的流通。在物流系统中,高可靠性与低成本是主要设计目的。对于基站 $i$,我们定义其“可靠性” $R_i$ 如下:
设物流基站 $i$ 有 $w$ 个前驱基站 $P_1,P_2,...P_w$ ,即这些基站以 $i$ 为后继基站,则基站 $i$ 的可靠性 $R_i$ 满足下式:
$R_i = C_i + k \sum_{j=1}^{w}R(P_j)$
其中 $C_i$ 和 $k$ 都是常实数且恒为正,且有 $k$ 小于 $1$。
整个系统的可靠性与控制基站的可靠性正相关,我们的目标是通过修改物流系统,即更改某些基站的后继基站,使得控制基站的可靠性 $R_1$尽量大。但由于经费限制,最多只能修改 $m$ 个基站的后继基站,并且,控制基站的后继基站不可被修改。因而我们所面临的问题就是,如何修改不超过 $m$ 个基站的后继,使得控制基站的可靠性 $R_1$ 最大化。
【输入格式】
第一行包含两个整数与一个实数:$N, m, k$。其中 $N$ 表示基站数目,$m$ 表示最多可修改的后继基站数目,$k$ 分别为可靠性定义中的常数。
第二行包含 $N$ 个整数,分别是 $S_1, S_2 … S_N$,即每一个基站的后继基站编号。
第三行包含 $N$ 个正实数,分别是 $C_1, C_2…C_N$,为可靠性定义中的常数。
【输出格式】
包含一个实数,为可得到的最大 $R_1$。精确到小数点两位。
【输入样例1】
4 1 0.5 2 3 1 3 10.0 10.0 10.0 10.0
【输出样例1】
30.00
【样例1说明】
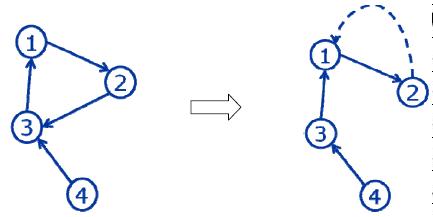
原有物流系统如图所示,$4$ 个物流基站的可靠性依次为 $22.8571,21.4286,25.7143,10$。
最优方案为将 $2$ 号基站的后继基站改为 $1$ 号,如右图所示。 此时 $4$ 个基站的可靠性依次为 $30,25,15,10$。
【样例2】
点击下载样例2
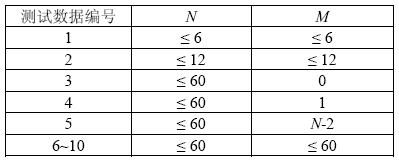
【数据规模和约定】
本题的数据,具有如下分布:
对于 $100\%$ 的数据,满足 $m ≤ N ≤ 60,C_i ≤ 10^6,0.3 ≤ k < 1$,请使用双精度实数,无需考虑由此带来的误差。