| 比赛场次 | 343 |
|---|---|
| 比赛名称 | 防止浮躁的小练习v0.9 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2016-11-07 08:00:00 |
| 结束时间 | 2016-11-07 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | NVIDIA |
| 注释介绍 |
| 题目名称 | 次小生成树 |
|---|---|
| 输入输出 | secmst.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAATTTTT | 5.313 s | 3.97 MiB | 50 |
【题目描述】
小 $C$ 最近学了很多最小生成树的算法,$Prim$ 算法、$Kurskal$ 算法、消圈算法等等。 正当小 $C$ 洋洋得意之时,小 $P$ 又来泼小 $C$ 冷水了。小 $P$ 说,让小 $C$ 求出一个无向图的次小生成树,而且这个次小生成树还得是严格次小的,也就是说: 如果最小生成树选择的边集是 $E_M$,严格次小生成树选择的边集是 $E_S$,那么需要满足:($value(e)$ 表示边 $e$ 的权值)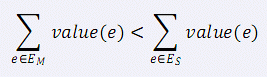 这下小 $C$ 蒙了,他找到了你,希望你帮他解决这个问题。大样例
这下小 $C$ 蒙了,他找到了你,希望你帮他解决这个问题。大样例
【输入格式】
第一行包含两个整数$N$和$M$,表示无向图的点数与边数。 接下来$M$行,每行$3$个数$x$ $y$ $z$ 表示,点 $x$ 和点 $y$ 之间有一条边,边的权值为 $z$。
【输出格式】
包含一行,仅一个数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
【样例输入】
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
【样例输出】
11
【提示】
数据中无向图无自环;
$50$% 的数据$N≤2000 , M≤3000$;
$80$% 的数据$N≤5,0000 , M≤10,0000$;
$100$% 的数据$N≤10,0000 , M≤30,0000$ ,边权值非负且不超过 $10^9$。
【来源】
$BZOJ$ $1977$