| 比赛场次 | 488 |
|---|---|
| 比赛名称 | 202110省实验桐柏一中普及组联赛 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2021-10-18 19:00:00 |
| 结束时间 | 2021-10-18 21:20:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 不爆零,得分就行。 |
| 题目名称 | 分配同桌 |
|---|---|
| 输入输出 | tongzhuo.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.002 s | 0.60 MiB | 100 |
|
|
AAAAAAAAAA | 0.002 s | 0.60 MiB | 100 |
|
|
AAAAAAAAAA | 0.007 s | 1.23 MiB | 100 |
|
|
AAAAAAAAAA | 0.024 s | 1.26 MiB | 100 |
|
|
AAAAAAAAAA | 0.029 s | 1.85 MiB | 100 |
|
|
AAAAAAAAAA | 0.367 s | 51.64 MiB | 100 |
|
|
AAAAAAAAAA | 0.625 s | 20.25 MiB | 100 |
|
|
AAAAAAAAAA | 0.753 s | 20.25 MiB | 100 |
|
|
AAAAAAAAAA | 0.772 s | 20.25 MiB | 100 |
|
|
AWWWAAWWAW | 0.000 s | 0.00 MiB | 40 |
|
|
AWWWAAWWAW | 0.826 s | 20.24 MiB | 40 |
|
|
WAWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
WAWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
WAWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
WAWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
WAWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
AWWWWWWWWW | 0.000 s | 0.00 MiB | 10 |
|
|
AWWWWWWWEE | 0.416 s | 1.34 MiB | 10 |
|
|
AWTTTTTTTT | 8.000 s | 80.96 MiB | 10 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
EEEEEEEEEE | 0.000 s | 0.00 MiB | 0 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
C | 0.000 s | 0.00 MiB | 0 |
|
|
WWWWWWWWWW | 0.003 s | 10.49 MiB | 0 |
【题目描述】
某班有若干个性格各异的大佬,大致可以分为外向的和内向的。为了使同学们相互学习,班主任决定重排座位,使尽量多对同桌的性格为一个外向一个内向,问最多可以安排几对这样的同桌。
同桌都是两两坐,因此每个人最多只能有$1$个同桌。
【输入格式】
输入文件有若干行:
第一行,两个整数$n$与$m$,表示共有$n$个同学$(10<=n<=10000)$,其中有$m$名同学是外向的;
接下来有若干行,每行有$2$个数字$a,b$。表示外向的$a$和内向的$b$可以坐同桌。(可能有重复)
注:外向的编号在前,且所有外向的编号都小于内向的编号,即外向的编号:$1$~$m$
内向的编号:$m+1$~$n$.
【输出格式】
输出文件有一行,包含$1$个整数,表示最多能匹配的同桌对数。
【样例输入】
10 5 1 6 1 8 2 6 3 6 3 7 4 8 4 9 4 10 4 10 5 8 5 9 [为了方便,样例数据从小到大给出,真实数据不一定如此]
【样例输出】
5
【样例说明】
如图中的$1,2,…,10$就代表$10$个同学,其中$1,2,3,4,5$是外向的,$6,7,8,9,10$是内向的。如果一个外向的同学和一个内向的同学可以做同桌,就在他们两个之间连一条线,两个人不能做同桌,就不连。注意:因为班主任很严格,两个外向的同学或两个内向的同学都一定不能做同桌.
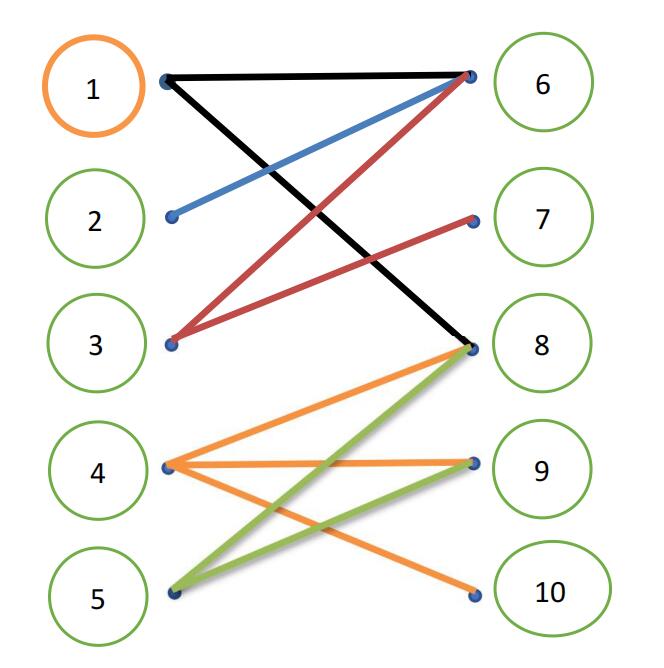
最大匹配方式可能不唯一,如图[实线表示匹配,虚线表示不匹配],一共匹配了$5$对同学,所有输出$5$。

【数据规模与约定】
$30$%的数据,$10<=n<=30;$
$50$%的数据,$10<=n<=50;$
$80$%的数据,$10<=n<=1000;$
$100$%的数据,$10<=n<=10000;$
【来源】
$dht@sywb$
$20211018$实验文博桐柏一中普及组联赛