| 比赛场次 | 524 |
|---|---|
| 比赛名称 | EYOI与SBOI开学欢乐赛8th |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-09-26 19:00:00 |
| 结束时间 | 2022-09-26 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | 该账号已注销 |
| 注释介绍 | 嘿嘿,啊哈哈哈哈! 哼,哼,啊啊啊啊啊啊啊!!! 第二题最简单捏!大家人均AK捏! |
| 题目名称 | 矩形覆盖 |
|---|---|
| 输入输出 | jxfg.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 7 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAA | 0.060 s | 0.82 MiB | 100 |
|
|
AAWAATA | 1.091 s | 1.64 MiB | 71 |
|
|
WAWWTTW | 2.107 s | 3.29 MiB | 14 |
【题目描述】
在平面上有 $n$ 个点,每个点用一对整数坐标表示。例如:当 $n=4$ 时,$4$ 个点的坐标分另为:$p_1(1,1),p_2(2,2),p_3(3,6),p_4(0,7)$,见图一。
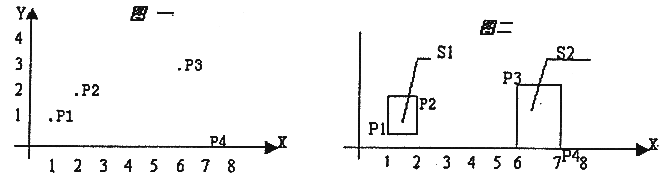
这些点可以用 $k$ 个矩形全部覆盖,矩形的边平行于坐标轴。当 $k=2$ 时,可用如图二的两个矩形 $s_l,s_2$ 覆盖,$s_1,s_2$ 面积和为 $4$。问题是当 $n$ 个点坐标和 $k$ 给出后,怎样才能使得覆盖所有点的 $k$ 个矩形的面积之和为最小呢。
约定:
覆盖一个点的矩形面积为 $0$;
覆盖平行于坐标轴直线上点的矩形面积也为 $0$;
各个矩形必须完全分开(边线与顶点也都不能重合)。
【输入格式】
$n$ $k$
$x_l$ $y_1$
$x_2$ $y_2$
... ...
$x_n$ $y_n$
【输出格式】
一个整数,即满足条件的最小的矩形面积之和。
【输入样例1】
4 2 1 1 2 2 3 6 0 7
【输出样例1】
4
【输入/输出样例2】
输入输出样例2
【数据规模与约定】
对于 $70 \%$ 的数据, 保证 $n \leq 15$;
对于 $100 \%$ 的数据,保证 $n \leq 50,1 \leq k \leq 4,0 \leq x_i,y_i \leq 500$;