| 比赛场次 | 356 |
|---|---|
| 比赛名称 | test2 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2017-03-12 18:00:00 |
| 结束时间 | 2017-03-12 20:40:00 |
| 开放分组 | 全部用户 |
| 组织者 | coco |
| 注释介绍 | 贪心图论动态规划练习 |
| 题目名称 | Geodetic 集合 |
|---|---|
| 输入输出 | geo.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.000 s | 0.00 MiB | 100 |
|
|
AAAAAAAAAA | 0.000 s | 0.00 MiB | 100 |
|
|
AAAAAAAAAA | 0.006 s | 0.32 MiB | 100 |
|
|
AAAAAAAAAA | 0.007 s | 0.32 MiB | 100 |
|
|
AAAAAAAAAA | 0.011 s | 0.32 MiB | 100 |
|
|
AAAAAAAAAA | 0.012 s | 0.33 MiB | 100 |
|
|
AAAAAAAAAA | 0.020 s | 0.32 MiB | 100 |
|
|
AAAAAAAAAA | 0.024 s | 0.81 MiB | 100 |
|
|
AAAAAAAAAA | 0.030 s | 0.81 MiB | 100 |
|
|
AAAAAAAAAA | 0.037 s | 0.33 MiB | 100 |
|
|
C | 0.000 s | 0.00 MiB | 0 |
【题目描述】
图G是一个无向连通图,没有自环,并且两点之间至多只有一条边。我们定义顶点v,u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点,这些顶点的集合记作I(v, u)。
我们称集合I(v, u)为一个Geodetic集合。
例如下图中,I(2, 5)={2, 3, 4, 5},I(1, 5)={1, 3, 5},I(2, 4)={2, 4}。
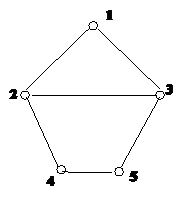
给定一个图G和若干点对v,u,请你分别求出I(v, u)。
【输入格式】
第一行两个整数n,m,分别表示图G的顶点数和边数(顶点编号1-n)
下接m行,每行两个整数a,b表示顶点a和b之间有一条无向边。
第m+2行有一个整数k,表示给定的点对数。
下接k行,每行两个整数v,u。
【输出格式】
共k行,每行对应输入文件中每一个点对v,u,按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。
【样例输入】
5 6 1 2 1 3 2 3 2 4 3 5 4 5 3 2 5 5 1 2 4
【样例输出】
2 3 4 5 1 3 5 2 4
【提示】
100%的数据,n<=40