| 比赛场次 | 538 |
|---|---|
| 比赛名称 | 4043级NOIP2022欢乐赛6th |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-11-18 18:40:00 |
| 结束时间 | 2022-11-18 22:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 从明天起,早睡早起,把最充沛的精力释放在NOIP时段。 |
| 题目名称 | 屠龙勇士 |
|---|---|
| 输入输出 | dragon.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
WWWWWWWWWWWWWWWWWWWW |
0.000 s | 0.00 MiB | 0 |
|
|
TTTTTTTTTTTTWTTTTTTT |
39.644 s | 24.81 MiB | 0 |
【题目描述】
小 $D$ 最近在网上发现了一款小游戏。游戏的规则如下:
•游戏的目标是按照编号 $1 \sim n$ 顺序杀掉 $n$ 条巨龙,每条巨龙拥有一个初始的生命值 $a_i$。同时每条巨龙拥有恢复能力,当其使用恢复能力时,它的生命值就会每次增加 $p_i$,直至生命值非负。只有在攻击结束后且当生命值恰好为 $0$ 时它才会死去。
•游戏开始时玩家拥有 $m$ 把攻击力已知的剑,每次面对巨龙时,玩家只能选择一把剑,当杀死巨龙后这把剑就会消失,但作为奖励,玩家会获得全新的一把剑。
小 $D$ 觉得这款游戏十分无聊,但最快通关的玩家可以获得 $ION2018$ 的参赛资格,于是小 $D$ 决定写一个笨笨的机器人帮她通关这款游戏,她写的机器人遵循以下规则:
•每次面对巨龙时,机器人会选择当前拥有的,攻击力不高于巨龙初始生命值中攻.击力最大的一把剑作为武器。如果没有这样的剑,则选择攻击力最低的一把剑作为武器。
•机器人面对每条巨龙,它都会使用上一步中选择的剑攻击巨龙固定的 $x$ 次,使巨龙的生命值减少 $x × ATK$。
•之后,巨龙会不断使用恢复能力,每次恢复 $p_i$ 生命值。若在使用恢复能力前或某一次恢复后其生命值为 $0$ ,则巨龙死亡,玩家通过本关。
那么显然机器人的攻击次数是决定能否最快通关这款游戏的关键。小 $D$ 现在得知了每条巨龙的所有属性,她想考考你,你知道应该将机器人的攻击次数 $x$ 设置为多少,才能用最少的攻击次数通关游戏吗?
当然如果无论设置成多少都无法通关游戏,输出 $-1$ 即可。
【输入格式】
第一行一个整数 $T$ ,代表数据组数。接下来 $T$ 组数据,每组数据包含 $5$ 行。
•每组数据的第一行包含两个整数,$n$ 和 $m$ ,代表巨龙的数量和初始剑的数量;
•接下来一行包含 $n$ 个正整数,第 $i$ 个数表示第 $i$ 条巨龙的初始生命值 $a_i$;
•接下来一行包含 $n$ 个正整数,第 $i$ 个数表示第 $i$ 条巨龙的恢复能力 $p_i$;
•接下来一行包含 $n$ 个正整数,第 $i$ 个数表示杀死第 $i$ 条巨龙后奖励的剑的攻击力;
•接下来一行包含 $m$ 个正整数,表示初始拥有的 $m$ 把剑的攻击力。
【输出格式】
输出文件一共 $T$ 行:
第 $i$ 行一个整数,表示对于第 $i$ 组数据,能够使得机器人通关游戏的最小攻击次数 $x$ ,如果答案不存在,输出$-1$。
【样例 1 输入】
2 3 3 3 5 7 4 6 10 7 3 9 1 9 1000 3 2 3 5 6 4 8 7 1 1 1 1 1
【样例 1 输出】
59 -1
【样例 1 解释】
第一组数据:
• 开始时拥有的剑的攻击力为 $\{1,9,10\}$,第 $1$ 条龙生命值为 $3$,故选择攻击力为 $1$ 的剑,攻击 $59$ 次,造成 $59$ 点伤害,此时龙的生命值为 $-56$,恢复 $14$ 次后生命值恰好为 $0$,死亡。
• 攻击力为 $1$ 的剑消失,拾取一把攻击力为 $7$ 的剑,此时拥有的剑的攻击力为
$\{7,9,10\}$,第 $2$ 条龙生命值为 $5$,故选择攻击力为 $7$ 的剑,攻击 $59$ 次,造成 $413$
点伤害,此时龙的生命值为 $-408$,恢复 $68$ 次后生命值恰好为 $0$,死亡。
• 此时拥有的剑的攻击力为 $\{3,9,10\}$,第 $3$ 条龙生命值为 $7$,故选择攻击力为 $3$ 的剑,攻击 $59$ 次,造成 $177$ 点伤害,此时龙的生命值为 $-170$,恢复 $17$ 次后生命值恰好为 $0$,死亡。
• 没有比 $59$ 次更少的通关方法,故答案为 $59$。
第二组数据:
• 不存在既能杀死第一条龙又能杀死第二条龙的方法,故无法通关,输出$-1$。
【样例 2 输入输出】
点击下载样例2
【数据规模与约定】
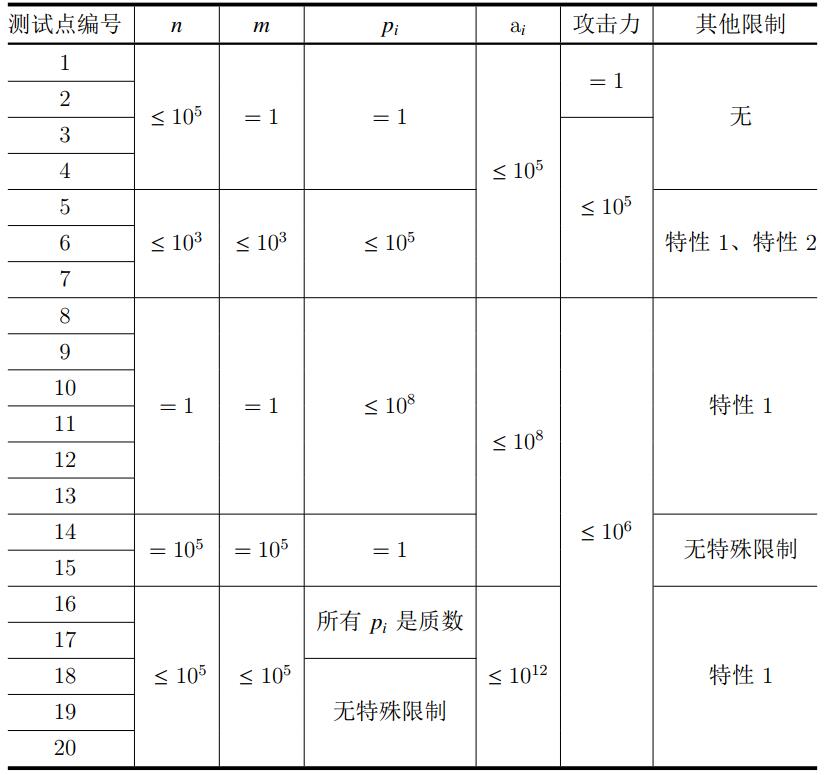
特性 $1$ 是指:对于任意的 $i, a_i ≤ p_i$。
特性 $2$ 是指: $LCM(p_i) ≤ 10^6$ 即所有 $p_i$ 的最小公倍数不大于 $10^6$。
对于所有的测试点, $T ≤ 5$ ,所有武器的攻击力 $≤ 10^6$ ,所有 $p_i$ 的最小公倍数$≤ 10^{12}$。
【提示】
你所用到的中间结果可能很大,注意保存中间结果的变量类型。