| 比赛场次 | 270 |
|---|---|
| 比赛名称 | 东方版NOIP模拟赛 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2015-10-28 18:30:00 |
| 结束时间 | 2015-10-28 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | cstdio |
| 注释介绍 | 出题人:月亮中学@dashgua 题目以幻想乡为背景,人物及团体均为虚构 pdf版题面:http://pan.baidu.com/s/1eQsbyhk 密码:s43r 题解:http://pan.baidu.com/s/1hq76Zha |
| 题目名称 | Marisa |
|---|---|
| 输入输出 | card.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AWWWWWWWWW | 0.002 s | 0.29 MiB | 10 |
|
|
AWWWWWWWWW | 0.003 s | 0.32 MiB | 10 |
|
|
AWWWWWWWWW | 0.003 s | 0.32 MiB | 10 |
|
|
AWWWWWWWWW | 0.014 s | 0.32 MiB | 10 |
|
|
WWWWWWWWWW | 0.002 s | 0.31 MiB | 0 |
|
|
WWWWWWWWWW | 0.003 s | 0.31 MiB | 0 |
【题目背景】
幻想乡的魔法使,雾雨魔理沙,发明了一种有趣的魔法卡片。
这种魔法卡片为正方形,分成若干个大小相同的方格,每个方格上都有一种印记,印记分为两种:"绮罗印记" 和 "幽光印记"。卡片上每一行,每一列的方格中都有两个 "绮罗印记",其他方格为 "幽光印记"。
这种卡片的神奇之处就在于,你可以任意次数地交换任意两行的所有方格,或者交换任意两列的所有方格。如果两张卡片可以通过这种行列交换变成相同的卡片,我们就认为它们是相同的。
琪露诺希望知道在一定尺寸下,共有多少种不同的魔法卡片,你能告诉他吗?
【题目描述】
给定正整数 $n$ ,对于一个 $n\times n$ 的01矩阵,如果每行元素之和都为 2,且每列元素之和都为 2,我们就称它是“可调整的”。
如果两个“可调整的”矩阵可以通过若干次交换矩阵的两行或两列变成相同的,我们认为它们是等价的“可调整的”矩阵。
求不同的“可调整的”矩阵的个数,输出答案对 998244353 取模的结果。
注意有多组数据。
【输入格式】
第一行一个正整数 $T$,表示数据组数。
接下来$T$行,每行一个正整数 $n$,表示矩阵的大小。
【输出格式】
应包含$T$行,每行一个数,表示你的答案。
【输入样例1】
1 2
【输出样例1】
1
【样例1解释】
当$n = 3$ 时有 1 种方案:
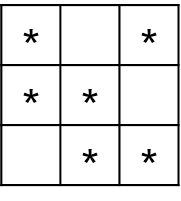
【输入样例2】
2 3 4
【输出样例2】
1 2
【样例2解释】
当$n = 4$ 时有 2 种方案:
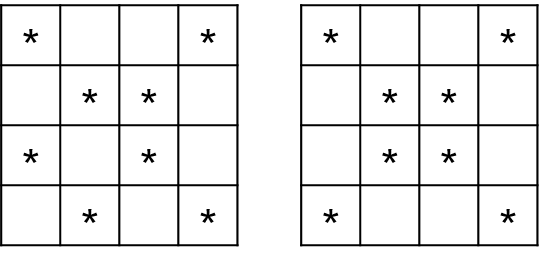
【数据范围与约定】
对于前 20% 的数据,$1\leq n\leq 7$;
对于前 40% 的数据,$1\leq n\leq 10$;
对于前 70% 的数据,$1\leq n\leq 100$;
对于 100% 的数据,$1\leq n\leq 1000,T\leq 10$。