| 比赛场次 | 630 |
|---|---|
| 比赛名称 | 9.27练习赛 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-09-27 18:30:00 |
| 结束时间 | 2024-09-27 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | HXF |
| 注释介绍 | 难度:4<3<2<1 |
| 题目名称 | 观光旅游 |
|---|---|
| 输入输出 | sightseeing.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 64 MiB |
| 测试点数 | 12 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAAAA | 1.061 s | 3.78 MiB | 100 |
|
|
AAAAAAAAAAAA | 1.065 s | 3.53 MiB | 100 |
|
|
AAAAAAAAAAAA | 1.076 s | 3.66 MiB | 100 |
|
|
AAAAAAAAAAAA | 1.220 s | 5.92 MiB | 100 |
|
|
AAAAAAAAAAAA | 1.258 s | 3.97 MiB | 100 |
|
|
AAAAAAAAAAAA | 2.608 s | 4.22 MiB | 100 |
|
|
AAAAAAAAAAAA | 2.661 s | 3.45 MiB | 100 |
|
|
AAAAAAAAAAAT | 3.159 s | 51.10 MiB | 92 |
|
|
AAAAAAAAAATT | 6.064 s | 4.29 MiB | 83 |
|
|
AATTTAATAATT | 18.024 s | 3.53 MiB | 50 |
|
|
AMATMAAMWTTT | 13.941 s | 51.00 MiB | 33 |
|
|
AWWTTTTTTEEE | 19.130 s | 3.67 MiB | 8 |
|
|
WWWTWWWTWWTT | 12.035 s | 3.67 MiB | 0 |
【题目描述】
本题面由 @数声风笛离亭晚 翻译。
$Your$ $Personal$ $Holiday$ 旅行社组织了一场游览比荷卢三国的巴士观光之旅,每一天,观光巴士从城市$S$开往城市$F$。通过这样,游客们可以看到沿途的美丽风景。另外,该观光巴士在一些风景优美的城市有停靠站( 0 个或更多),方便游客下车去景点游玩。
不同的游客群体可能对他们想要观看的景点有不同的偏好,因此从$S$到$F$的路线也会时常更改。$Your$ $Personal$ $Holiday$ 旅行社希望为客户提供多种
不同路线的选择,由于酒店已提前预订,因此起始城市$S$和最终城市$F$是固定不变的。如果沿途中从城市$A$到城市$B$的至少一条道路是一条路线的一部分,而不是另一条路线的一部为了留出足够的时间在车站观光(并避免使用太多的燃料),游客可以选择的路线也有限制,观光巴士必须选择$S$到$F$的较短路线,它必须是具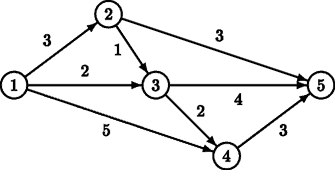 有最短路线,或者是比最短路长一个距离单位的路线。实际上,若通过比最短路线距离稍长的路线,游客可能会有更多的选择,而不是将它们限制在最短路线上。这样可以增强游客们的观景体验。
有最短路线,或者是比最短路长一个距离单位的路线。实际上,若通过比最短路线距离稍长的路线,游客可能会有更多的选择,而不是将它们限制在最短路线上。这样可以增强游客们的观景体验。
以该地图为例,从城市$S$到城市$F$($S = 1, F = 5$)的最短路径有两条,分别为$ 1 → 2 → 5 $和$ 1 → 3 → 5 $,其长度均为$ 6 $。还有一条长度比最短路线长一个单位距离的路线,为$ 1 → 3 → 4 → 5 $,其长度为$ 7 $。现在,有好几张比荷卢三国的(部分)地图,起点城市$S$和终点城市$F$。$Your$ $Personal$ $Holiday$ 旅行社想知道按照以上路线选择方法,有多少种不同的路线可以提供给游客们。
【输入格式】
每个输入文件包含多组数据。
输入文件的第一行,包含一个正整数$T$,代表该输入文件中所含的数据组数。
接下来是$T$组数据,每组数据的格式如下:
第一行包含两个整数$N$和$M$,两个数之间以一个空格分开,分别代表城市的数量和地图上道路的个数。
接下来的$M$行,每行包含三个整数$A$、$B$和$L$,每个数之间以一个空格分开,代表从$A$城市到达$B$城市的路径长度为$L$.这些道路是单向的。因此,如果有从城市$A$到城市$B$的道路,但不一定有从城市$B$到城市$A$的道路,但不排除测试数据中提供双向道路的情况。
第 $M+2$ 行包含两个整数$S$和$F$,两个数之间以一个空格分开,代表本次观光游览的起点城市与终点城市。
保证存在至少一条可以从城市$S$到达城市$F$的路线。
【输出格式】
输出文件包含$T$行,分别对应$T$组数据的答案,每组数据的答案格式如下:
一个整数,表示最短路径和长度比最短路径长 $1$ 单位路径的路径的数量和。
【样例输入】
2 5 8 1 2 3 1 3 2 1 4 5 2 3 1 2 5 3 3 4 2 3 5 4 4 5 3 1 5 5 6 2 3 1 3 2 1 3 1 10 4 5 2 5 2 7 5 2 7 4 1
【样例输出】
3 2
【提示】
第一个测试数据对应着题目描述中的图片。由于输入量较大,建议使用$sacnf()$代替$C++$中的$cin$;
对于加强后的数据,测试点满足以下性质:

对于 $100\%$ 的数据,保证有:
$2≤N≤1×10^3, 1≤M≤1×10^4, 1≤A,B≤N, A≠B, 1≤L≤1×10^3, 1≤S,F≤N, S≠F, T≤300.$
【来源】