| 比赛场次 | 549 |
|---|---|
| 比赛名称 | 2022级数学专题练习赛8 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2023-02-06 18:40:00 |
| 结束时间 | 2023-02-06 22:10:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 以赛代练 |
| 题目名称 | 奇怪的背包 |
|---|---|
| 输入输出 | knapsack.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 1.192 s | 17.08 MiB | 100 |
|
|
AAAAAAAAAA | 1.278 s | 5.17 MiB | 100 |
题目描述
小 $C$ 非常擅长背包问题,他有一个奇怪的背包,这个背包有一个参数 $P$,当他向这个背包内放入若干个物品后,背包的重量是物品总体积对 $P$ 取模后的结果。
现在小 $C$ 有 $n$ 种体积不同的物品,第 $i$ 种占用体积为 $V_i$,每种物品都有无限个。他会进行 $q$ 次询问,每次询问给出重量 $w_i$,你需要回答有多少种放入物品的方案,能将一个初始为空的背包的重量变为 $w_i$。注意,两种方案被认为是不同的,当且仅当放入物品的种类不同,而与每种物品放入的个数无关。不难发现总的方案数为 $2^n$。
由于答案可能很大,你只需要输出答案对 $10^9+7$ 取模的结果。
输入格式
第一行三个整数 $n,q,P$。
接下来一行 $n$ 个整数表示 $V_i$。
接下来一行 $q$ 个整数表示 $w_i$。
输出格式
输出 $q$ 行,每行一个整数表示答案。
【样例1输入】
3 3 6 1 3 4 5 2 3
【样例1输出】
5 6 6
【样例1解释】
对于第一个询问 $5$,选择 $\{1\},\{1,3\},\{1,4\},\{3,4\},\{1,3,4\}$ 都是合法的方案。
【样例2】
点击下载样例2
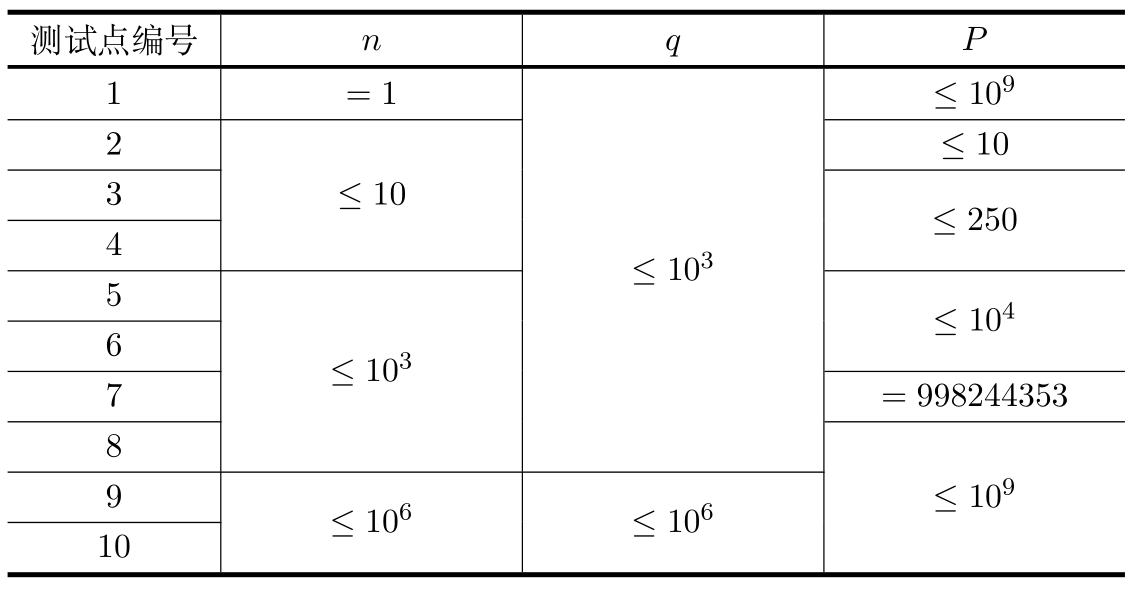
【数据范围与约定】
对于所有数据,有 $1\le n, q\le 10^6, 3\le P\le 10^9, 0\lt V_i,w_i\lt P$。
保证 $V_i$ 两两不同。