| 比赛场次 | 558 |
|---|---|
| 比赛名称 | 2022级DP专题练习赛8 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2023-03-01 18:30:00 |
| 结束时间 | 2023-03-01 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 做好今天,昨天勿扰 |
| 题目名称 | 网络收费 |
|---|---|
| 输入输出 | networkcost.in/out |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【问题描述】
网络已经成为当今世界不可或缺的一部分。每天都有数以亿计的人使用网络进行学习、科研、娱乐等活动。然而,不可忽视的一点就是网络本身有着庞大的运行费用。所以,向使用网络的人进行适当的收费是必须的,也是合理的。
$MY$ 市 $NS$ 中学就有着这样一个教育网络。网络中的用户一共有 $2^N$ 个,编号依次为 $1, 2, 3, …, 2^N$。这些用户之间是用路由点和网线组成的。用户、路由点与网线共同构成一个满二叉树结构。树中的每一个叶子结点都是一个用户,每一个非叶子结点(灰色)都是一个路由点,而每一条边都是一条网线(见下图,用户结点中的数字为其编号)。
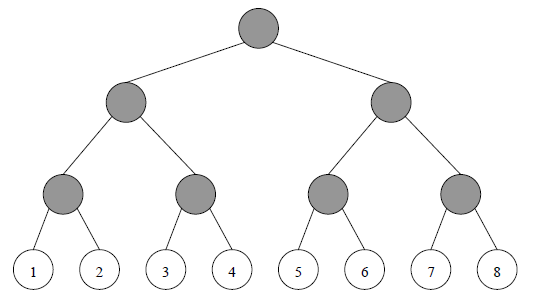
$MY$ 网络公司的网络收费方式比较奇特,称为“ 配对收费 ”。即对于每两个用户 $i, j (1≤i < j ≤2^N )$ 进行收费。由于用户可以自行选择两种付费方式 $A、B$ 中的一种,所以网络公司向学校收取的费用与每一位用户的付费方式有关。该费用等于每两位不同用户配对产生费用之和。
为了描述方便,首先定义这棵网络树上的一些概念:
- 祖先:根结点没有祖先,非根结点的祖先包括它的父亲以及它的父亲的祖先;
- 管辖叶结点:叶结点本身不管辖任何叶结点,非叶结点管辖它的左儿子所管辖的叶结点与它的右儿子所管辖的叶结点;
- 距离:在树上连接两个点之间的用边最少的路径所含的边数。
对于任两个用户 $i, j (1≤i<j≤2^N )$,首先在树上找到与它们距离最近的公共祖先:路由点 $P$,然后观察 $P$ 所管辖的叶结点(即用户)中选择付费方式 $A$ 与 $B$ 的人数,分别记为 $n_A$ 与 $n_B$,接着按照网络管理条例第 $X$ 章第 $Y$ 条第 $Z$ 款进行收费(如下表),其中 $F_{i,j}$ 为 $i$ 和 $j$ 之间的流量,且为已知量。
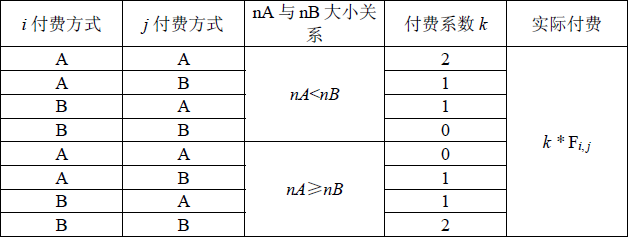
由于最终所付费用与付费方式有关,所以 $NS$ 中学的用户希望能够自行改变自己的付费方式以减少总付费。然而,由于网络公司已经将每个用户注册时所选择的付费方式记录在案,所以对于用户 $i$,如果他/她想改变付费方式(由 $A$ 改为 $B$ 或由 $B$ 改为 $A$),就必须支付 $C_i$ 元给网络公司以修改档案(修改付费方式记录)。
现在的问题是,给定每个用户注册时所选择的付费方式以及 $C_i$,试求这些用户应该如何选择自己的付费方式以使得 $NS$ 中学支付给网络公司的总费用最少(更改付费方式费用+配对收费的费用)。
【输入格式】
输入文件中第一行有一个正整数 $N$。
第二行有 $2^N$ 个整数,依次表示 $1$ 号,$2$ 号,…,$2^N$ 号用户注册时的付费方式,每一个数字若为 `0`,则表示对应用户的初始付费方式为 $A$,否则该数字为 `1`,表示付费方式为 $B$。
第三行有 $2^N$ 个整数,表示每一个用户修改付费方式需要支付的费用,依次为 $C_1$, $C_2$, …,$C_M$。( M=$2^N$ )
以下 $2^N-1$ 行描述给定的两两用户之间的流量表 $F$,总第 $(i + 3)$ 行第 $j$ 列的整数为 $F_{i, j+i}$ 。$(1≤i<2^N,1≤j≤2^N – i)$
所有变量的含义可以参见题目描述。
【输出格式】
你的程序只需要向输出文件输出一个整数,表示 $NS$ 中学支付给网络公司的最小总费用。(单位:元)
【样例1输入】
2 1 0 1 0 2 2 10 9 10 1 2 2 1 3
【样例1输出】
8
【样例2】
点击下载样例2
【样例说明】
将 $1$ 号用户的付费方式由 $B$ 改为 $A$,$NS$ 中学支付给网络公司的费用达到最小。
【评分方法】
本题没有部分分,你的程序的输出只有和我们的答案完全一致才能获得满分,否则不得分。
【数据规模和约定】
对于 $40\%$ 的数据,$N≤4$;
对于 $80\%$ 的数据,$N≤7$;
对于 $100\%$ 的数据,$N≤10,0≤F_{i, j}≤500,0≤C_i≤500 000$。