| 比赛场次 | 399 |
|---|---|
| 比赛名称 | 2017noip |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2017-09-20 19:00:00 |
| 结束时间 | 2017-09-21 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | Hyoi_ctime |
| 注释介绍 |
| 题目名称 | 组合数问题 |
|---|---|
| 输入输出 | problem.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAAAAAAAAAAAA |
0.551 s | 30.84 MiB | 100 |
|
|
AAAAAAAAAAAAAAAAAAAA |
0.710 s | 30.95 MiB | 100 |
|
|
AAAAAAAAAAAAAAAAAAAA |
0.730 s | 68.98 MiB | 100 |
|
|
AAAAAAAAAAAAAAAAAAAA |
0.909 s | 30.99 MiB | 100 |
|
|
AAAAAAAAAAAAAAAAAAAA |
1.264 s | 61.96 MiB | 100 |
|
|
AAAAAAAAAAAAAAAWAAAA |
0.394 s | 31.40 MiB | 95 |
|
|
ATATATATATATATATATAT |
10.153 s | 31.14 MiB | 50 |
|
|
ATATATATATATATATATAT |
10.173 s | 31.14 MiB | 50 |
|
|
AAAAAAAAAWWWWWWTEEEE |
1.955 s | 0.31 MiB | 45 |
|
|
EEEEEEEEEEEEEEEEEEEE |
1.388 s | 68.05 MiB | 0 |
【题目描述】
组合数 $C_n^m$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子,从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 $C_n^m$ 的一般公式:
$C_n^m=\frac{n!}{m!(n-m)!}$
其中 $n!=1\times2\times\cdots\times n$;特别地,定义 $0 != 1$。
小葱想知道如果给定 $n,m$ 和 $k$,对于所有的 $0\leq i\leq n,0\leq j\leq \min(i,m)$ 有多少对 $(i,j)$ 满足 $C_i^j$ 是 $k$ 的倍数。
【输入格式】
第一行有两个整数 $t, k$,其中 $t$ 代表该测试点总共有多少组测试数据,$k$ 的意义见【问题描述】。
接下来 $t$ 行每行两个整数 $n,m$,其中 $n,m$ 的意义见【问题描述】。
【输出格式】
$t$ 行,每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min(i,m)$ 中有多少对 $(i, j)$ 满足 $C_i^j$ 是 $k$ 的倍数。
【样例1输入】
1 2 3 3
【样例1输出】
1
【提示】
在所有可能的情况中,只有$C_2^1$是 $2$ 的倍数。
【样例2输入】
2 5 4 5 6 7
【样例2输出】
0 7
【数据范围】
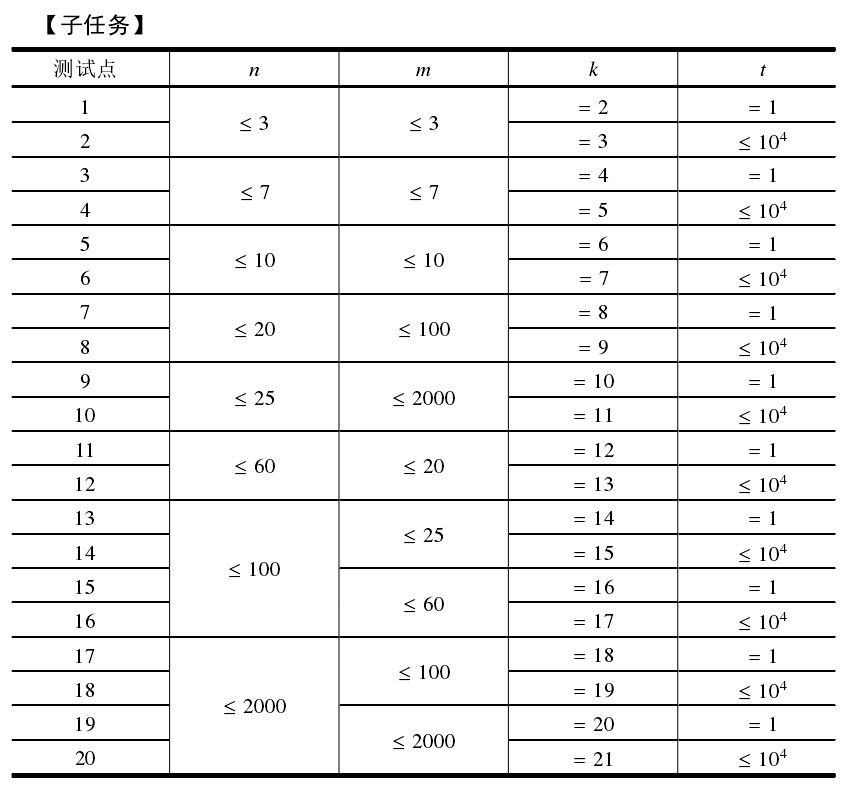
【来源】
$NOIP2016\ Day2\ Task1$