| 比赛场次 | 431 |
|---|---|
| 比赛名称 | 近期练习题回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2018-10-16 09:00:00 |
| 结束时间 | 2018-11-01 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 题目陆续增多 |
| 题目名称 | 过路费 |
|---|---|
| 输入输出 | toll.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 16 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.793 s | 14.16 MiB | 100 |
|
|
AAAAAAAAAA | 0.888 s | 14.18 MiB | 100 |
【题目描述】
跟所有人一样,农夫约翰以着宁教我负天下牛,休教天下牛负我(原文:宁我负人,休教人负我)的伟大精神,日日夜夜苦思生财之道。为了发财,他设置了一系列的规章制度,使得任何一只奶牛在农场中的道路行走,都要向农夫约翰上交过路费。
农场中由$N(1 <= N <= 250)$片草地(标号为$1$到$N$),并且有$M(1 <= M <= 10000)$条双向道路连接草地$A_j$和$B_j(1 <= A_j <= N; 1 <= B_j <= N)$。奶牛们从任意一片草地出发可以抵达任意一片的草地。FJ已经在连接$A_j$和$B_j$的双向道路上设置一个过路费$L_j(1 <= L_j <= 100,000)$。
可能有多条道路连接相同的两片草地,但是不存在一条道路连接一片草地和这片草地本身。最值得庆幸的是,奶牛从任意一片草地出发,经过一系列的路径,总是可以抵达其它的任意一片草地。
除了贪得无厌,FJ都不知道该说什么好。FJ竟然在每片草地上面也设置了一个过路费$C_i(1 <= C_i <= 100000)$。从一片草地到另外一片草地的费用,是经过的所有道路的过路费之和,加上经过的所有的草地(包括起点和终点)的过路费的最大值。
任劳任怨的牛们希望去调查一下她们应该选择那一条路径。她们要你写一个程序,接受$K(1 <= K <= 10,000)$个问题并且输出每个询问对应的最小花费。第i个问题包含两个数字$s_i和t_i(1 <= s_i <= N; 1 <= t_i <= N; s_i != t_i)$,表示起点和终点的草地。
考虑下面这个包含5片草地的样例图像:
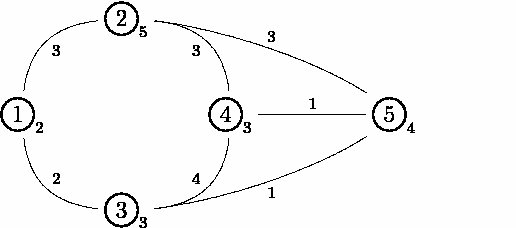
从草地$1$到草地$2$的道路的“边过路费”为$3$,草地$2$的“点过路费”为$5$。
要从草地$1$走到草地$4$,可以从草地$1$走到草地$3$再走到草地$5$最后抵达草地$4$。如果这么走的话,需要的“边过路费”为$2+1+1=4$,需要的点过路费为$4$(草地$5$的点过路费最大),所以总的花费为$4+4=8$。
而从草地$2$到草地$3$的最佳路径是从草地$2$出发,抵达草地$5$,最后到达草地$3$。这么走的话,边过路费为$3+1=4$,点过路费为$5$,总花费为$4+5=9$。
【输入格式】
* 第$1$行: 三个空格隔开的整数: $N, M,K$
* 第$2$到第$N+1$行: 第$i+1$行包含一个单独的整数: $C_i$
* 第$N+2$到第$N+M+1$行: 第$j+N+1$行包含$3$个由空格隔开的整数: $A_j, B_j,L_j$
* 第$N+M+2$倒第$N+M+K+1$行: 第$i+N+M+1$行表示第$i$个问题,包含两个由空格隔开的整数$s_i$和$t_i$
【输出格式】
* 第$1$到第$K$行: 第$i$行包含一个单独的整数,表示从$s_i$到$t_i$的最小花费。
【样例输入】
5 7 2 2 5 3 3 4 1 2 3 1 3 2 2 5 3 5 3 1 5 4 1 2 4 3 3 4 4 1 4 2 3
【样例输出】
8 9
【来源】
$USACO Dec 09$