| 比赛场次 | 655 |
|---|---|
| 比赛名称 | 2025.1.14 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2025-01-14 19:00:00 |
| 结束时间 | 2025-01-14 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | HXF |
| 注释介绍 | 考不过省一线的写反省! |
| 题目名称 | 树的遍历 |
|---|---|
| 输入输出 | traverse.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 25 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
WWWWWWWWWWWWWWWWWAWW WWWWW |
0.079 s | 3.44 MiB | 4 |
|
|
WWWWWWWWWWWWWWWWWAWW WWWWW |
0.086 s | 3.38 MiB | 4 |
|
|
WWWWWWWWWWWWWWWWWAWW WWWWW |
0.131 s | 3.51 MiB | 4 |
|
|
WWWEEEWWWWWWWWWWWAWW WWWWW |
1.084 s | 3.59 MiB | 4 |
|
|
WWWWWWWWWWWWWWWWWWWW WWWWW |
0.075 s | 3.33 MiB | 0 |
|
|
WWWWWWWWWWWWWWWWWWWW WWWWW |
0.077 s | 3.39 MiB | 0 |
|
|
WWWWWWWWWWWWWWWWWWWW WWWWW |
0.079 s | 3.33 MiB | 0 |
【题目描述】
小 Q 是一个算法竞赛初学者,正在学习图论知识中的树的遍历。一棵由 $n$ 个结点,$n - 1$ 条边构成的树,初始时所有结点都未被标记,它的遍历过程如下:
1. 选择一个结点 $s$ 作为遍历起始结点,并把该结点打上标记。
2. 假设当前访问的结点为 $u$,寻找任意一个与 $u$ 相邻且未标记的结点 $v$,将 $v$ 作为新的当前访问结点并打上标记。之后再次进入第 $2$ 步。
3. 假设在第 $2$ 步中,与 $u$ 相邻的结点都已被标记,如果 $u = s$ 则遍历过程结束,否则将 $u$ 设为遍历 $u$ 之前的上一个结点并再进入第 $2$ 步。
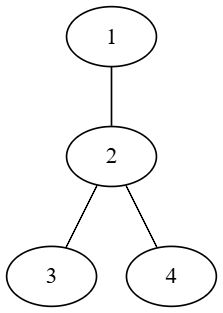
例如在下面的树中,一种可能的遍历过程如下:
选取 $1$ 作为遍历起始结点,并把 $1$ 打上标记;
$2$ 与 $1$ 相邻且未标记,将 $2$ 设为当前访问结点,并把 $2$ 打上标记。
$2$ 与 $3$ 相邻且未标记,将 $3$ 设为当前访问结点,并把 $3$ 打上标记。
$3$ 所有相邻的结点都被标记,将当前访问结点设为遍历结点 $3$ 之前的结点 $2$。
$2$ 与 $4$ 相邻且未标记,将 $4$ 设为当前访问结点,并把 $4$ 打上标记。
$4$ 所有相邻的结点都被标记,将当前访问结点设为遍历结点 $4$ 之前的结点 $2$。
$2$ 所有相邻的结点都被标记,将当前访问结点设为遍历结点 $2$ 之前的结点 $1$。
$1$ 所有相邻的结点都被标记,且 $1$ 是遍历起始结点,故遍历结束。
作为一个奇思妙想的学生,小 Q 在学习完上述知识后不满足于以结点为基础的遍历方式,于是开始研究以边为基础的遍历方式。定义两条边**相邻**,当且仅当它们有一个公共的结点。初始时,所有的边都未被标记。这种以边为基础的遍历过程如下:
1. 选择一条边 $b$ 作为遍历起始边,并把该边打上标记。
2. 假设当前访问边为 $e$,寻找任意一条与 $e$ 相邻且未标记的边 $f$,将 $f$ 作为新的当前访问边并打上标记。之后再次进入第 $2$ 步。
3. 假设在第 $2$ 步中,与 $e$ 相邻的边都已被标记,如果 $e = b$ 则遍历过程结束,否则将 $e$ 设为遍历 $e$ 之前的上一条边并再进入第 $2$ 步。
例如在上面的树中,一种可能的遍历过程如下(定义 $\{u, v\}$ 表示连接结点 $u$ 和 $v$ 的边):
选取 $\{1, 2\}$ 作为遍历起始边,并把 $\{1, 2\}$ 打上标记;
$\{1, 2\}$ 与 $\{2, 3\}$ 相邻且未标记,将 $\{2, 3\}$ 设为当前访问边,并把 $\{2, 3\}$ 打上标记。
$\{2, 3\}$ 与 $\{2, 4\}$ 相邻且未标记,将 $\{2, 4\}$ 设为当前访问边,并把 $\{2, 4\}$ 打上标记。
$\{2, 4\}$ 所有相邻的边都被标记,将当前访问边设为遍历 $\{2, 4\}$ 之前的边 $\{2, 3\}$。
$\{2, 3\}$ 所有相邻的边都被标记,将当前访问边设为遍历 $\{2, 3\}$ 之前的边 $\{1, 2\}$。
$\{1, 2\}$ 所有相邻的边都被标记,且 $\{1, 2\}$ 是遍历起始边,故遍历结束。
小 Q 惊奇的发现,在这个新的树的遍历过程中,如果将每条边看作一个新的结点,将步骤 $2$ 中的所有新结点 $e$ 和 $f$ 连接一条新边,就会生成一棵由 $n-1$ 个新结点和 $n-2$ 条新边连接成的新树。例如上述遍历过程得到的新树如下(新的结点和新边都用红色表示):
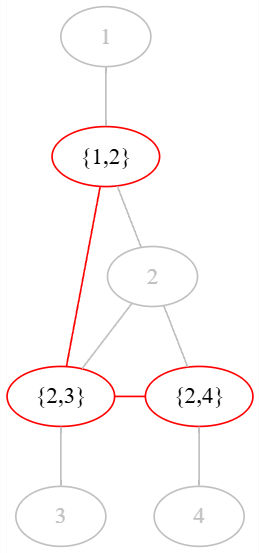
现在小 Q 在 $n - 1$ 条边中选择了 $k$ 条关键边。小 Q 想知道,以任意一条关键边作为起始遍历边,通过上述遍历过程能够生成多少种不同的新树。这里两棵树被认为是不同的,当且仅当至少存在某一对新的结点,它们仅在其中一棵树中连有新边。
由于结果可能很大,你只需要输出其对 $10^9+7$ 取模的结果即可。
【输入格式】
本题有多组测试数据。
输入的第一行包含两个整数 $c, T$,表示测试点的编号和测试数据的组数。在样例中,$c$ 表示该样例与测试点 $c$ 的数据范围相同。
接下来包含 $T$ 组数据,每组数据的格式如下:
·第一行包含两个整数 $n, k$,表示树的结点数以及小 Q 选择的关键边的数量。
·接下来 $n - 1$ 行,第 $i$ 行包含两个整数 $u_i, v_i$,表示树上编号为 $i$ 的边连接结点 $u_i$ 和 $v_i$。
·接下来一行包含 $k$ 个整数 $e_1, e_2, \dots, e_k$,表示小 Q 选择的关键边的编号。保证关键边的编号互不相同。
【输出格式】
对于每组测试数据输出一行,包含一个整数,表示结果对 $10^9 + 7$ 取模的结果。
【样例1输入】
1 1 4 1 1 2 2 3 2 4 1
【样例1输出】
2
【样例1说明】
两种可能的新树如下:
新结点 $\{1, 2\}$ 和新结点 $\{2, 3\}$ 连新边,新结点 $\{2, 3\}$ 和新结点 $\{2, 4\}$ 连新边。
新结点 $\{1, 2\}$ 和新结点 $\{2, 4\}$ 连新边,新结点 $\{2, 4\}$ 和新结点 $\{2, 3\}$ 连新边。
【样例2输入】
7 1 5 2 1 2 1 3 2 4 2 5 1 3
【样例2输出】
3
【样例2说明】
三种可能的新树如下:
新结点 $\{1, 2\}$ 和 $\{1, 3\}$,$\{1, 2\}$ 和 $\{2, 4\}$,$\{2, 4\}$ 和 $\{2, 5\}$ 之间分别连新边。该新树可以选择 $\{1, 2\}$ 作为起始遍历边得到。
新结点 $\{1, 2\}$ 和 $\{1, 3\}$,$\{1, 2\}$ 和 $\{2, 5\}$,$\{2, 5\}$ 和 $\{2, 4\}$ 之间分别连新边。该新树可以选择 $\{1, 2\}$ 或 $\{2, 4\}$ 作为起始遍历边得到。
新结点 $\{1, 2\}$ 和 $\{1, 3\}$,$\{1, 2\}$ 和 $\{2, 4\}$,$\{1, 2\}$ 和 $\{2, 5\}$ 之间分别连新边。该新树可以选择 $\{2, 4\}$ 作为起始遍历边得到。
【样例 3】
见选手目录下的 traverse/traverse3.in 与 traverse/traverse3.ans。
该组样例满足 $c = 4$。
【样例 4】
见选手目录下的 traverse/traverse4.in 与 traverse/traverse4.ans。
该组样例满足 $c = 7$。
【样例 5】
见选手目录下的 traverse/traverse5.in 与 traverse/traverse5.ans。
该组样例满足 $c = 11$。
【样例 6】
见选手目录下的 traverse/traverse6.in 与 traverse/traverse6.ans。
该组样例满足 $c = 13$。
【样例 7】
见选手目录下的 traverse/traverse7.in 与 traverse/traverse7.ans。
该组样例满足 $c = 15$。
【样例 8】
见选手目录下的 traverse/traverse8.in 与 traverse/traverse8.ans。
该组样例满足 $c = 16$。
【样例 9】
见选手目录下的 traverse/traverse9.in 与 traverse/traverse9.ans。
该组样例满足 $c = 18$。
【样例 10】
见选手目录下的 traverse/traverse10.in 与 traverse/traverse10.ans。
该组样例满足 $c = 19$。
【样例 11】
见选手目录下的 traverse/traverse11.in 与 traverse/traverse11.ans。
该组样例满足 $c = 22$。
【样例 12】
见选手目录下的 traverse/traverse12.in 与 traverse/traverse12.ans。
该组样例满足 $c = 24$。
【数据规模与约定】
对于所有的测试数据,保证:
$1 \leq T \leq 10$;
$2 \leq n \leq 10^5$;
$1 \leq k < n$;
对于任意的 $i(1 \leq i \leq n - 1)$,都有 $1 \leq u_i, v_i \leq n$,且构成一颗合法的树。
对于任意的 $i(1 \leq i \leq k)$,都有 $1 \leq e_i < n$,且两两不同。
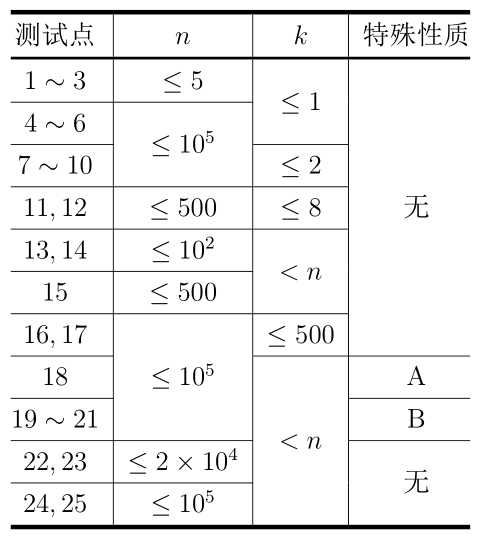
特殊性质 A:对于任意的 $i(1 \leq i \leq n - 1)$,都有 $u_i = i, v_i = i + 1$。
特殊性质 B:对于任意的 $i(1 \leq i \leq n - 1)$,都有 $u_i = 1, v_i = i + 1$。
【提示】
数据输入的规模可能较大,请选手注意输入读取方式的效率。