| 比赛场次 | 297 |
|---|---|
| 比赛名称 | 20160329 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2016-03-29 08:40:00 |
| 结束时间 | 2016-03-29 11:40:00 |
| 开放分组 | 全部用户 |
| 组织者 | mouse |
| 注释介绍 |
| 题目名称 | 拉拉队 |
|---|---|
| 输入输出 | Cheerleaders.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.014 s | 1.46 MiB | 100 |
|
|
AAAAAAAAAA | 0.023 s | 2.58 MiB | 100 |
|
|
AAAAAAAAAA | 0.024 s | 2.20 MiB | 100 |
|
|
WWWWWWWWWW | 0.032 s | 2.26 MiB | 0 |
【题目描述】
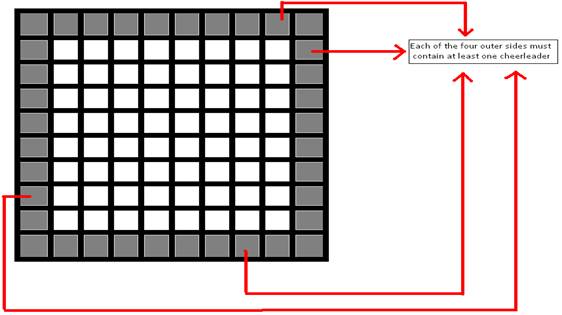
在大多数专业的体育赛事中,拉拉队总是对观众的娱乐起着相当大的作用(尤其是在休息时,并开始玩之前)世界杯足球也不例外。通常情况下,拉拉队员们组成一个小组,并在场地中央表演,有时她们中有些人被置于边缘以便更接近观众。组织者希望确保每个边至少有一名拉拉队员。对于这个问题,我们将场地建模为一个 $M*N$ 个矩形网格,共有 $k$ 名队员。用于放置拉拉队的限制说明如下:
$*\ 4$ 条边上每条边至少有一名拉拉队员。需要注意的是,放置一个拉拉队员在一个角落里的网格中相当于同时涵盖两条边。
$*$ 一个网格中最多有一名队员。
$*$ 所有可用的啦啦队必须被分配给一个网格。也就是说,没有队员可以被排除在外(处于闲置状态)。
【输入格式】
输入第一行为数据组数 $T(T ≤ 50)$,每组数据包含 $3$ 个整数 $m ,n , k(2≤m,n≤20,k≤500)$.
【输出格式】
对于每组数据,输出总方案数除以 $1 000 007$ 的余数。
【样例输入】
2 2 2 1 2 3 2
【样例输出】
Case 1: 0 Case 2: 2
【提示】
相当于:
在一个 $m$ 行 $n$ 列的矩形网格里放 $k$ 个石子,问有多少种放法?每个格子里最多放一个石子,所有石子都要用完,并且第一行,最后一行,第一列,最后一列都得有石子。
【来源】
$UVa$ $11806$ $Cheerleaders.$
刘汝佳,《算法竞赛入门经典训练指南》表2.2