| 比赛场次 | 634 |
|---|---|
| 比赛名称 | 2024国庆练习3 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-10-06 14:30:00 |
| 结束时间 | 2024-10-06 18:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | HXF |
| 注释介绍 | 部分分给的很足! |
| 题目名称 | 划分 |
|---|---|
| 输入输出 | partition.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 1024 MiB |
| 测试点数 | 25 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAAAAAAAAAAAA AAEEE |
2.348 s | 13.36 MiB | 88 |
|
|
AAAAAAAAAAAAAAAAAAAA AATTT |
15.505 s | 6.18 MiB | 88 |
|
|
AAAAAAAAAAAAAAAAAAAA AATTT |
15.612 s | 8.16 MiB | 88 |
|
|
AAAAAAAAAAAAAAAAEEEE EEEEE |
13.819 s | 126.06 MiB | 64 |
|
|
AAAAAAAAAAAAAAAATTTT TTWWW |
30.223 s | 5.52 MiB | 64 |
|
|
AAAAAAAAATTTTTTTEEEE EEEEE |
39.174 s | 194.37 MiB | 36 |
|
|
AAAAAAAAATTTTTTTTTTT TTTTT |
80.122 s | 35.56 MiB | 36 |
|
|
TWWTTTTTTAWWWWWWTTTT TTTTT |
79.996 s | 3.22 MiB | 4 |
|
|
TTTTTTTTTAWWWWWWTTTT TTTTT |
89.989 s | 3.21 MiB | 4 |
【题目描述】
2048 年,第三十届 CSP 认证的考场上,作为选手的小明打开了第一题。这个题的样例有 $n$ 组数据,数据从 $1 \sim n$ 编号,$i$ 号数据的规模为 $a_i$。
小明对该题设计出了一个暴力程序,对于一组规模为 $u$ 的数据,该程序的运行时间为 $u^2$。然而这个程序运行完一组规模为 $u$ 的数据之后,它将在任何一组规模小于 $u$ 的数据上运行错误。样例中的 $a_i$ 不一定递增,但小明又想在不修改程序的情况下正确运行样例,于是小明决定使用一种非常原始的解决方案:将所有数据划分成若干个数据段,段内数据编号连续,接着将同一段内的数据合并成新数据,其规模等于段内原数据的规模之和,小明将让新数据的规模能够递增。
也就是说,小明需要找到一些分界点 $1 \leq k_1 \lt k_2 \lt \cdots \lt k_p \lt n$,使得
$$ \sum_{i=1}^{k_1} a_i \leq \sum_{i=k_1+1}^{k_2} a_i \leq \cdots \leq \sum_{i=k_p+1}^{n} a_i$$
注意 $p$ 可以为 $0$ 且此时 $k_0 = 0$,也就是小明可以将所有数据合并在一起运行。
小明希望他的程序在正确运行样例情况下,运行时间也能尽量小,也就是最小化
$$ (\sum_{i=1}^{k_1} a_i)^2 + (\sum_{i=k_1+1}^{k_2} a_i)^2 + \cdots + (\sum_{i=k_p+1}^{n} a_i)^2 $$
小明觉得这个问题非常有趣,并向你请教:给定 $n$ 和 $a_i$,请你求出最优划分方案下,小明的程序的最小运行时间。
【输入格式】
由于本题的数据范围较大,部分测试点的 $a_i$ 将在程序内生成。
第一行两个整数 $n, type$。$n$ 的意义见题目描述,$type$ 表示输入方式。
1. 若 $type = 0$,则该测试点的 $a_i$ 直接给出。输入文件接下来:第二行 $n$ 个以空格分隔的整数 $a_i$,表示每组数据的规模。
2. 若 $type = 1$,则该测试点的 $a_i$ 将特殊生成,生成方式见后文。输入文件接下来:第二行六个以空格分隔的整数 $x, y, z, b_1, b_2, m$。接下来 $m$ 行中,第 $i (1 \leq i \leq m)$ 行包含三个以空格分隔的正整数 $p_i, l_i, r_i$。
对于 $type = 1$ 的 23~25 号测试点,$a_i$ 的生成方式如下:
给定整数 $x, y, z, b_1, b_2, m$,以及 $m$ 个三元组 $(p_i, l_i, r_i)$。
保证 $n \geq 2$。若 $n \gt 2$,则 $\forall 3 \leq i \leq n, b_i = (x \times b_{i−1} + y \times b_{i−2} + z) \mod 2^{30}$。
保证 $1 \leq p_i \leq n, p_m = n$。令 $p_0 = 0$,则 $p_i$ 还满足 $\forall 0 \leq i \lt m$ 有 $p_i \lt p_{i+1}$。
对于所有 $1 \leq j \leq m$,若下标值 $i (1 \leq i \leq n)$满足 $p_{j−1} \lt i \leq p_j$,则有
$a_i = \left(b_i \mod \left( r_j − l_j + 1 \right) \right) + l_j$
上述数据生成方式仅是为了减少输入量大小,标准算法不依赖于该生成方式。
【输出格式】
输出一行一个整数,表示答案。
【样例输入1】
5 0 5 1 7 9 9
【样例输出1】
247
【样例输入2】
10 0 5 6 7 7 4 6 2 13 19 9
【样例输出2】
1256
【样例输入3】
10000000 1 123 456 789 12345 6789 3 2000000 123456789 987654321 7000000 234567891 876543219 10000000 456789123 567891234
【样例输出3】
4972194419293431240859891640
【样例解释】
【样例 1 解释】
最优的划分方案为 $\{5,1\}, \{7\}, \{9\}, \{9\}$。由 $5 + 1 \leq 7 \leq 9 \leq 9$ 知该方案合法。
答案为 $(5 + 1)^2 + 7^2 + 9^2 + 9^2 = 247$。
虽然划分方案 $\{5\}, \{1\}, \{7\}, \{9\}, \{9\}$ 对应的运行时间比 $247$ 小,但它不是一组合法方案,因为 $5 \gt 1$。
虽然划分方案 $\{5\}, \{1,7\}, \{9\}, \{9\}$ 合法,但该方案对应的运行时间为 $251$,比 $247$ 大。
【样例 2 解释】
最优的划分方案为 $\{5\}, \{6\}, \{7\}, \{7\}, \{4,6,2\}, \{13\}, \{19,9\}$。
【数据规模与约定】
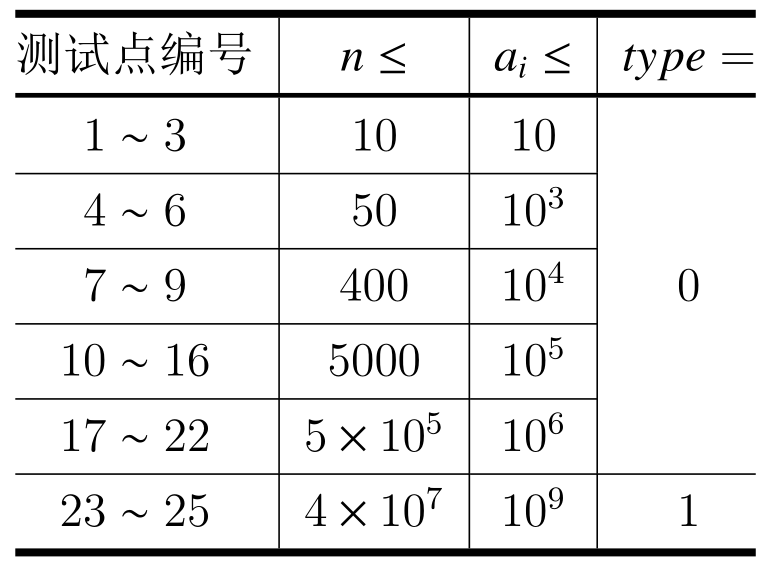
所有测试点满足:$type\in\{0,1\},2\leq n\leq 4\times 10^7, 1\leq a_i\leq10^9,1\leq m\leq 10^5,$
$1\leq l_i \leq r_i\leq10^9,0\leq x,y,z,b_1,b_2<2^{30}$。
【来源】
CSP-S 2019 Day2 Task 2