| 比赛场次 | 393 |
|---|---|
| 比赛名称 | 不平凡的世界 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2017-09-05 19:00:00 |
| 结束时间 | 2017-09-05 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | cqw |
| 注释介绍 |
| 题目名称 | 不平凡的许愿树 |
|---|---|
| 输入输出 | hopetree.in/out |
| 时间限制 | 5000 ms (5 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.492 s | 0.47 MiB | 100 |
|
|
AAAAAAAAAA | 0.755 s | 0.62 MiB | 100 |
|
|
AAAAATTTTT | 25.242 s | 96.04 MiB | 50 |
|
|
AAAEEEEEEE | 0.527 s | 0.36 MiB | 30 |
|
|
AAWWWWWTTT | 17.637 s | 191.93 MiB | 20 |
【题目描述】
noip要到了,大家来到许愿树前。这个许愿树不仅仅是许愿树,还有未卜先知的功能。众OIer问许愿树:“不平凡的许愿树,CCF告诉我们noip中会有两道题目从Openjudge上选择,你能不能告诉我是哪两道题。”
许愿树想了想直接说出答案并不妥:“中国有句古话叫‘闷声大发财’,我就什么也不说,这是最好的。但是我看到你们这么热情,一句话不说也不好,我就告诉你们点信息吧。你们看我是一个由N个结点组成的树,在树中任选着3个点,有多少种选择方案使得这三个点互相之间的距离相同?两个方案不同当且仅当一个点在第一种方案中被选择,第二种方案中没有被选择。”
“记你算出来方案数为cnt,那么第一道题的题号就是cnt%338 + 1,第二题的题目编号是(cnt+233)%338+1。”
可是OIer们手头并没有计算机,于是请你来告诉他们题目编号。
【输入格式】
第一行一个整数N,表示树有N个点。
接下来N-1行,每行两个整数u,v,表示树中有一条从u到v的边
【输出格式】
一行,两个整数,分别为预测的第一题题号和第二题题号。
【样例输入】
7 1 2 5 7 2 5 2 3 5 6 4 5
【样例输出】
6 239
【提示】
样例解释:
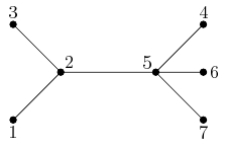
共有5种方案,分别是{1,3,5},{2,4,6},{2,4,7},{2,6,7},{4,6,7}。所以第一题的编号为5%338 + 1 = 6;第二题的编号为(5+233)%338 + 1 = 239;
数据范围与约定:
对于30%的数据:1 <= n <= 100
对于60%的数据:1 <= n <= 1500
对于100%的数据:1 <= n <= 5000
胡扯:
其实Openjudge没有确切题号,第1.1节有10题,第1.2节有10题...,不如约定第16题的编号是第1.2节的第6题。如果命中我什么都不知道。
【来源】
在此键入。