| 比赛场次 | 496 |
|---|---|
| 比赛名称 | SBOI虎年首秀 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-02-23 19:00:00 |
| 结束时间 | 2022-02-23 21:20:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 此SB非彼SB,SBOI:2019级文博初中神犇OIers |
| 题目名称 | 一级方程式赛车 |
|---|---|
| 输入输出 | formula1.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAAATATAAAAAA |
2.811 s | 2.84 MiB | 90 |
【题目描述】
无论现实情况是什么样的,我们假设$Vologda$市无法取得$20**$年冬季奥运会的主办权,众所周知,这个城市将举办$F1$赛事之一。显然,为了举办这场重要的比赛,宾馆,餐厅,国际机场和一条新的赛道——为了将涌入这座城市的F1粉丝们的需要所有设施——将被修建。但当所有的宾馆和一半的餐厅建成之后,人们发现了一个问题:在赛道的规划位置上有许多地鼠在打洞。因为我们非常喜爱小动物,生态学家们决不会同意在这些洞上修建赛道。因此,市长现在苦恼地坐在他的办公室里,看着标注了所有地鼠洞的赛道规划地图。
谁会足够聪明,来设计一条赛道来避免这座城市的耻辱吗?当然,只有真正的专家——当地蓝翔技校久经沙场的程序员们!但我们的英雄们没有就此满足,而是提出了一个更难的问题:“显然,如果我们找到修筑赛道的方案总数,我们的市长将很自豪!”他们说。
必须要说的是,$Vologda$市的赛道将会相当简单。赛道将是一条穿过$N*M$矩形所有网格的单回路。每一段都和某个矩形的边平行,因此弯道都将是直角。在下图中,给出了$N=M=4$时的两种修筑方案(灰色格子意味着地鼠洞,粗黑线就是赛道)。在下图中没有其他的修建方案。
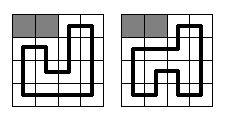
【输入格式】
输入文件的第一行包含两个正整数$N,M(2<=N,M<=12)$。
接下来的$N$行,每行包含$M$个字符,描述了矩形中相应的网格。字符“.”意味着应当修建赛道的网格,而字符“*”意味着有地鼠打洞的网格。
【输出格式】
输出一行一个正整数,即修筑赛道的方案总数。假设这个数不超过$2^{63}-1$。
【样例输入1】
4 4 **.. .... .... ....
【样例输出1】
2
【样例输入2】
4 4 .... .... .... ....
【样例输出2】
6
【提示】
赛道必须是一条单回路,这意味着赛道不能被分成互不相连的若干个部分。
【来源】
Problem Author: Nikita Rybak, Ilya Grebnov, Dmitry Kovalioff
Problem Source: Timus Top Coders: Third Challenge