| 比赛场次 | 648 |
|---|---|
| 比赛名称 | 20241128 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-11-28 07:30:00 |
| 结束时间 | 2024-11-28 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | syzhaoss |
| 注释介绍 |
| 题目名称 | 魔法卡片 |
|---|---|
| 输入输出 | magic.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAATAAAATTTTTTTTTTTT |
28.510 s | 76.37 MiB | 35 |
|
|
TTTEEEWWTTTTEEEEEEEE |
16.298 s | 5.24 MiB | 0 |
|
|
TTTTEWWETTTTTTTTTTTT |
32.477 s | 3.40 MiB | 0 |
【题目描述】
有$n$张卡片,每张卡片有正反两面。正面和反面一共有$1,2,\cdots,m$这$m$个数,有些数在正面,有些在反面,但是不会有数同时存在于两个面。这$n$张卡片排成一排,标号为$1,2,\cdots,n$。
进行$Q$次询问,每次给出两个数$l,r(l\leq r)$,定义$f(l,r)$为所有在第$l,l+1,\cdots,r$张卡片的正面出现过的数的平方和。 你可以随意将卡片翻面,使得$f(l,r)$最大化,输出这个值。
例如有$3$张卡片且$m=5$,这些卡片上的数字如下图:
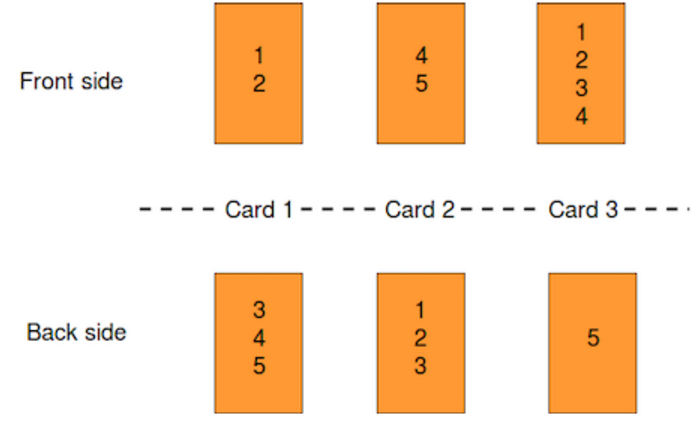
如果$l=1,r=2$,那么如果不翻卡片,那么我们有$1,2,4,5$在正面,它们的平方和为$46$。
如果我们将第$1$张卡片翻面,那么在正面的数字有$3,4,5$,它们的平方和为$50$。
如果我们将第$1,2$张卡片反面,那么在正面的数字有$1,2,3,4,5$,它们的平方和为$55$,这也是$f(1,2)$的最大值。大樣例
【输入格式】
第一行,一共三个数,表示$n,m,Q$。
接下来$n$行,每行第一个数$x_i$,表示正面有$x_i$个数,接下来$x_i$个$1$到$m$之间不同的数。
接下来$Q$行,每行两个数$l,r$。
【输出格式】
对于每组询问,输出一个数表示答案。
【样例1输入】
2 3 2 2 2 1 2 2 3 1 1 1 2
【样例1输出】
9 14
【样例1说明】
对于询问$l=1,r=1$,只有一张卡片,如果不翻面,平方和为$1^2+2^2=5$,如果翻面,平方和为$3^2=9$。
对于询问$l=1,r=2$,不需要反面,平方和为$1^2+2^2+3^2=14$。
【样例2输入】
2 5 1 3 4 2 1 2 4 3 1 2
【样例1输出】
50
【数据规模与约定】
对于$20\%$的数据,$m\leq 10$。
对于$40\%$的数据,$m\leq 200$。
对于$60\%$的数据,$m\leq 1024$。
对于$100\%$的数据,$1\leq n\times m,Q\leq 10^6,0\leq x_i\leq m,1\leq l\leq r\leq n$。
2019.3.1