| 比赛场次 | 519 |
|---|---|
| 比赛名称 | EYOI与SBOI开学欢乐赛3rd |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-09-05 19:00:00 |
| 结束时间 | 2022-09-05 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | op_组撒头屯 |
| 注释介绍 | 有思路的,细心点儿,争取多拿分; 没思路的,大胆点儿,争取拿到分; |
| 题目名称 | van玩galgame |
|---|---|
| 输入输出 | galgame.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.808 s | 12.60 MiB | 100 |
|
|
AAAAAAAAAA | 0.961 s | 21.75 MiB | 100 |
|
|
AAAAAAAAAA | 2.878 s | 51.51 MiB | 100 |
|
|
AAAAAAAAAA | 3.671 s | 66.77 MiB | 100 |
|
|
AAAAAAAAAA | 3.933 s | 75.35 MiB | 100 |
|
|
AAWWWWWTTT | 4.366 s | 43.88 MiB | 20 |
|
|
WWWWWWWWWW | 2.782 s | 20.32 MiB | 0 |
【题目背景】
四季轮换,光阴如梭,又到了 $van$ 玩galgame的时候……
【题目描述】
提示:题目描述的最后提供了一份简要的、形式化描述的题面。
galgame一般的玩法是由玩家完成一个故事,中途会出现不同的选项,例如对话的应对和前往的地点,这些选项会触发不同的事件,因此会有许多的剧情支线,产生不同的结局,我们将这些岔口和结局称为关键节点。例如,下图是某galgame的流程图:
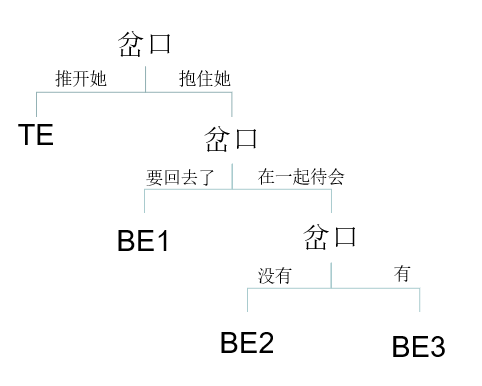
$van$ 玩的这款galgame完成某个结局的方案是唯一的,也就是像上图一样构成一棵树,共有 $n$ 个关键节点,但不保证是二叉树。
$van$ 是个感性的人,他在玩galgame时总会将自己的真情实感带入游戏,于是他对各个选项的看法不同。具体的,$van$ 若在某个岔口选择了某个选项,他将会获得对应的快乐值 $p$ ,快乐值可能为负数,这代表 $van$ 厌恶这个选项。
这款galgame贴心的设计了存档功能,但因为种种原因只能使用一次。具体的,$van$ 可以在游玩过程中的任意时刻存档,并在存档后任意时刻读档回到存档时的位置,他可以借此选择另外的选项并进入其他线路。但是,若 $van$ 读档后选择了与之前相同的选项,他不会再次获得相应的快乐值。当然,$van$ 也可以选择不使用存档功能。
现在 $van$ 要开始玩这款galgame了,他一定从根节点开始,但不一定要完成某个结局才读档或停止,请你帮他算算,他能获得的最多快乐值为多少?
形式化题面:
给定一棵 $n$ 个节点的树,每条边有可正可负的边权,要求先以根节点为一端选择一条简单路径,再以所选路径上一点为端选择一条没有重叠的简单路径,使得两条路径的总权值最大。
【输入格式】
第一行一个正整数 $n$
接下来 $n$ 行,第 $i$ 行首先一个非负整数 $k_i$ 。
若 $k_i≠0$ ,则第 $i$ 个关键节点为岔口,$k_i$ 表示岔口的选项个数,接下来 $2k_i$ 个数,每两个一组,第 $j$ 组的两个数分别表示选择第 $j$ 个选项的快乐值 $p$ 和选择后的下一个关键节点 $s$ 。
若 $k_i=0$ ,则表示这是一个结局。
【输出格式】
一个非负整数,表示 $van$ 能获得的最大快乐值。
【样例输入】
7 2 3 2 4 3 0 2 4 4 5 5 0 2 -10 6 -15 7 0 0
【样例输出】
13
【样例说明】
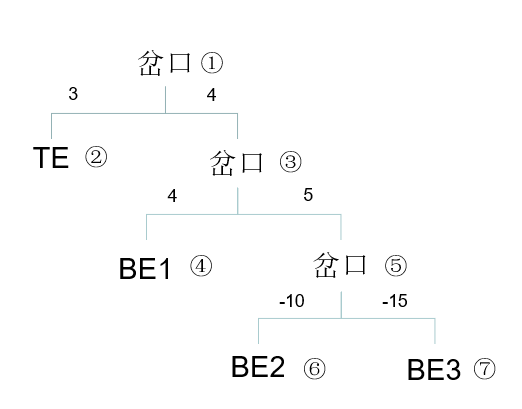
最优方案是:1-3(存档)-5-3(读档)-4
获得 13 点快乐值
【数据规模与约定】
对于$40\%$的数据,$1≤n≤1000$
对于$100\%$的数据,$1≤n≤10^6$
$|p|≤10^9$
保证根节点为 $1$
【提示】
输入量较大,如果你不会写快读:
inline int read(){
int ans=0,sgn=1;
char ch=getchar();
while(!isdigit(ch)){
if (ch=='-')sgn=-1;
ch=getchar();
}
while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
return ans*sgn;
}
【来源】
$rsr$