| 比赛场次 | 514 |
|---|---|
| 比赛名称 | EYOI暨SBOI暑假快乐赛4th |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-28 08:30:00 |
| 结束时间 | 2022-06-28 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | op_组撒头屯 |
| 注释介绍 | EYOI暨SBOI2022暑假的第四场比赛! 暑假热身赛第四,题都很难哦! 粗心审题,尽力丢掉可以拿到的分数! 注意题目难度是按照题目编号依次递增! |
| 题目名称 | 选题 |
|---|---|
| 输入输出 | mathproblem.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 1024 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAEEEEEEEE | 1.425 s | 4.74 MiB | 20 |
|
|
AAEEEEEEEE | 1.441 s | 4.74 MiB | 20 |
|
|
AAEEEEEEEE | 1.731 s | 4.77 MiB | 20 |
|
|
AAWEEEEEEE | 2.719 s | 26.39 MiB | 20 |
|
|
AAWWEEEEEE | 3.732 s | 211.82 MiB | 20 |
|
|
WWWWWWWWWW | 1.598 s | 2.91 MiB | 0 |
【题目描述】
上帝为了感谢$van$帮他修好了所有设备,派天使送给他$n$本互不相同的数学题,但$van$并不贪婪,打算拿走总共的$1/k$,也就是$n/k$个。在不同的平行宇宙中,$van$选择的$k$不相同,拿走的$n/k$本数学题也不相同,但保证$k$为$n$的正因数。这样,$van$的总方案数便是$P$。
简单来说,$P$=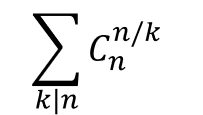 。
。
由于上帝认为$P$太大了,但不知道将$P$模一个什么数好,于是便有了$q$次询问。
对于每一次询问,上帝会在$1-m$间选择$s$个质数,第$i$个的编号$s_i$,表示从小到大数的第$s_i$个质数。上帝把它们乘起来,便得到了$Q$,接下来你需要替$van$回答:$P$%$Q$=?
【输入格式】
第一行三个正整数,$n$,$m$,$q$。
接下来$q$行,每行第一个数$s$,接下来$s$个数,第$i$个表示$s_i$。
【输出格式】
$q$行,每行一个正整数,表示答案,即$P$%$Q$。
【样例输入1】
4 5 2 1 2 2 1 3
【样例输出1】
2 1
【样例说明1】
$C_n^m$表示从$n$个不同元素中取出$m(m≤n)$个元素的所有组合的个数;
$4$的正因数有$1、2、4$,于是$P=C_4^4+C_4^2+C_4^1=1+6+4=11$。
$1$~$5$的质数有$2、3、5$。
第一次询问的$Q=3$,答案$P$%$Q=2$。
第二次询问的$Q=2*5=10$,答案$P$%$Q=1$。
【样例输入2】
12 7 4 2 1 3 2 3 4 3 1 2 4 4 1 2 3 4
【样例输出2】
8 3 38 38
【样例说明2】
$12$的正因数有$1、2、3、4、6、12$,于是:
$P=C_{12}^{12}+C_{12}^6+C_{12}^4+C_{12}^3+C_{12}^2+C_{12}^1 = 1+924+495+220+66+12=1718$,
$1$~$7$的质数有$2、3、5、7$。
第一次询问的$Q=2*5=10$,答案$P$%$Q=8$。
第二次询问的$Q=5*7=35$,答案$P$%$Q=3$。
第三次询问的$Q=2*3*7=42$,答案$P$%$Q=38$。
第四次询问的$Q=2*3*5*7=210$,答案$P$%$Q=38$。
【数据规模与约定】
对于20%的数据,$n<=20,m<=50,q<=50,Q<=100$。
对于100%的数据,$n<=10^7,m<=5×10^4,q<=10^3,Q<=5×10^7$。
【来源】
$rsr$