| 比赛场次 | 514 |
|---|---|
| 比赛名称 | EYOI暨SBOI暑假快乐赛4th |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-28 08:30:00 |
| 结束时间 | 2022-06-28 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | op_组撒头屯 |
| 注释介绍 | EYOI暨SBOI2022暑假的第四场比赛! 暑假热身赛第四,题都很难哦! 粗心审题,尽力丢掉可以拿到的分数! 注意题目难度是按照题目编号依次递增! |
| 题目名称 | 往广大的天空 |
|---|---|
| 输入输出 | stasis.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 1024 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAATWWWWTW | 2.323 s | 2.88 MiB | 30 |
|
|
AAAEEETTTT | 5.183 s | 4.59 MiB | 30 |
【题目背景】

“尘封已久的飞行器,却发出顺畅的运作声,
仿佛期待着飞往广大的天空。”
“菲希卡没有注意到,在装置下方正显示着一行红色的小字。
「注意:目的地已指定。不可更改。」”
【题目描述】
菲希卡试图通过研究飞行器上的装置来确定他们的目的地,但她发现装置的结构远远比她想象中的复杂。
装置的控制面板上有$n$个节点,$m$条线将它们连接起来。一条线有“亮”和“暗”两种状态,每秒钟,部分线的状态会发生改变,但总体不会和之前的任意一秒相同,当所有情况全部出现后,称为完成了一个“周期”。
现在,菲希卡要对$1$号节点进行“调律”,“调律”会顺着“亮”着的线蔓延到与之相连的节点。当节点间的连接情况变化时,“调律”的蔓延情况也会随之变化。
菲希卡想问你:对于$k∈[2,n]$,在一个“周期”中,总共存在多少秒,使得$k$节点拥有“调律”。答案对$998244353$取模。
【输入格式】
第一行,两个正整数$n,m$。
接下来$m$行,每行两个正整数$i,j$,表示节点$i,j$之间存在一条线。
【输出格式】
$n-1$个正整数,第$i$个表示$k=i+1$时的答案对$998244353$取模的值。
【样例输入】
4 4 1 2 1 3 2 3 1 4
【样例输出】
10 10 8
【样例说明】
一个“周期”,连线代表“亮”:
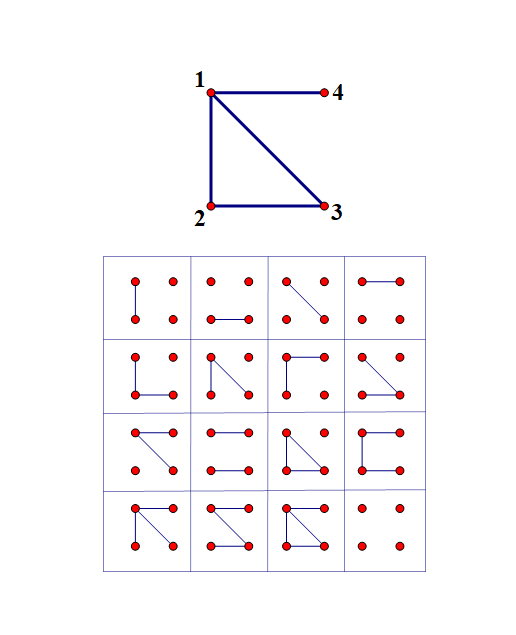
若以表格中从上到下,从左到右的顺序排时间:
$2$号节点拥有“调律”的时间是第$1,5,6,7,8,11,12,13,14,15$秒,共$10$秒。
$3$号节点拥有“调律”的时间是第$3,5,6,8,9,11,12,13,14,15$秒,共$10$秒。
$4$号节点拥有“调律”的时间是第$4,7,9,10,12,13,14,15$秒,共$8$秒。
【数据规模与约定】
保证没有重边或自环。
对于$30%$的数据,$n<=7$;
对于$100%$的数据,$n<=17,m<=n*(n-1)/2$;
【来源】
$rsr$