| 比赛场次 | 185 |
|---|---|
| 比赛名称 | NOIP 2012 Day1 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2012-11-10 08:30:00 |
| 结束时间 | 2012-11-10 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | 王者自由 |
| 注释介绍 |
| 题目名称 | 开车旅行 |
|---|---|
| 输入输出 | drive.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
小 $A$ 和小 $B$ 决定利用假期外出旅行,他们将想去的城市从 $1$ 到 $N$ 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 $i$ 的海拔高度为 $H_i$,城市 $i$ 和城市 $j$ 之间的距离 $d[i,j]$ 恰好是这两个城市海拔高度之差的绝对值,即$d[i, j] = |H_i − H_j|$。
旅行过程中,小$A$ 和小$B$ 轮流开车,第一天小$A$ 开车,之后每天轮换一次。他们计划选择一个城市 $S$ 作为起点,一直向东行驶,并且最多行驶 $X$ 公里就结束旅行。小 $A$ 和小$B$ 的驾驶风格不同,小$B$ 总是沿着前进方向选择一个最近的城市作为目的地,而小$A$ 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出X公里,他们就会结束旅行。
在启程之前,小$A$ 想知道两个问题:
1.对于一个给定的 $X=X_0$,从哪一个城市出发,小 $A$ 开车行驶的路程总数与小 $B $行驶的路程总数的比值最小(如果小 $B$ 的行驶路程为$0$,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小$A$ 开车行驶的路程总数与小$B$行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2.对任意给定的 $X=X_i$和出发城市 $S_i$,小 $A$ 开车行驶的路程总数以及小 $B$ 行驶的路程总数。
【输入格式】
第一行包含一个整数 $N$,表示城市的数目。
第二行有 $N$ 个整数,每两个整数之间用一个空格隔开,依次表示城市 $1$ 到城市 $N$ 的海拔高度,即$H_1,H_2,……,H_n$,且每个$H_i$都是不同的。
第三行包含一个整数 $X_0$。
第四行为一个整数 $M$,表示给定$M$组$S_i$和 $X_i$。
接下来的$M$行,每行包含$2$个整数$S_i$和$X_i$,表示从城市 $S_i$ 出发,最多行驶$X_i$公里。
【输出格式】
输出共 $M+1$ 行。
第一行包含一个整数$S_0$,表示对于给定的$X_0$,从编号为$S_0$的城市出发,小$A$开车行驶的路程总数与小$B$行驶的路程总数的比值最小。
接下来的 $M$ 行,每行包含 $2$ 个整数,之间用一个空格隔开,依次表示在给定的 $S_i$和$X_i$下小$A$行驶的里程总数和小$B$ 行驶的里程总数。
【样例输入 1】
4 2 3 1 4 3 4 1 3 2 3 3 3 4 3
【样例输出 1】
1 1 1 2 0 0 0 0 0
【输入输出样例 1 说明】
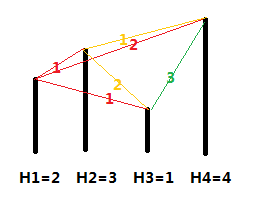
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市1出发, 可以到达的城市为$2,3,4$,这几个城市与城市 $1$ 的距离分别为 $1,1,2$,但是由于城市$3$的海拔高度低于城市 $2$,所以我们认为城市 $3$ 离城市 $1$ 最近,城市 $2$ 离城市 $1$ 第二近,所以小 $A$ 会走到城市 $2$。到达城市 $2$ 后,前面可以到达的城市为 $3,4$,这两个城市与城市 $2$ 的距离分别为 $2,1$,所以城市 $4$ 离城市 $2$ 最近,因此小 $B$ 会走到城市 $4$。到达城市$4$后,前面已没有可到达的城市,所以旅行结束。
如果从城市$2$出发,可以到达的城市为$3,4$,这两个城市与城市 $2$ 的距离分别为 $2,1$,由于城市$3$离城市$2$第二近,所以小$A$会走到城市 $3$。到达城市$3$后,前面尚未旅行的城市为$4$,所以城市 $4$ 离城市 $3$ 最近,但是如果要到达城市 $4$,则总路程为 $2+3=5>3$,所以小 $B$ 会直接在城市 $3$ 结束旅行。
如果从城市 $3$ 出发,可以到达的城市为 $4$,由于没有离城市 $3$ 第二近的城市,因此旅行还未开始就结束了。
如果从城市 $4$ 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【样例输入 2】
10 4 5 6 1 2 3 7 8 9 10 7 10 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7
【样例输出 2】
2 3 2 2 4 2 1 2 4 5 1 5 1 2 1 2 0 0 0 0 0
【输入输出样例 2 说明】
当 $X=7$时:
如果从城市$1$出发,则路线为 $1 -> 2 -> 3 -> 8 -> 9$,小$A$ 走的距离为$1+2=3$,小$B$走的距离为 $1+1=2$。(在城市 $1$ 时,距离小 $A$ 最近的城市是 $2$ 和 $6$,但是城市 $2$ 的海拔更高,视为与城市$1$第二近的城市,所以小$A$ 最终选择城市 $2$;走到$9$后,小$A$只有城市$10$ 可以走,没有第$2$选择可以选,所以没法做出选择,结束旅行)
如果从城市$2$出发,则路线为 $2 -> 6 -> 7$,小$A$ 和小$B$走的距离分别为 $2,4$。
如果从城市$3$出发,则路线为 $3 -> 8 -> 9$,小$A$和小$B$走的距离分别为 $2,1$。
如果从城市$4$出发,则路线为 $4 -> 6 -> 7$,小$A$和小$B$走的距离分别为 $2,4$。
如果从城市$5$出发,则路线为 $5 -> 7 -> 8$,小$A$和小$B$走的距离分别为 $5,1$。
如果从城市$6$出发,则路线为 $6 -> 8 -> 9$,小$A$和小$B$走的距离分别为 $5,1$。
如果从城市$7$出发,则路线为 $7 -> 9 -> 10$,小$A$和小$B$走的距离分别为 $2,1$。
如果从城市$8$出发,则路线为 $8 -> 10$,小$A$和小$B$走的距离分别为$2,0$。
如果从城市$9$出发,则路线为 $9$,小 $A$和小$B$走的距离分别为$0,0$(旅行一开始就结束了)。
如果从城市$10$出发,则路线为 $10$,小$A$和小$B$走的距离分别为$0,0$。
从城市 $2$ 或者城市 $4$ 出发小 $A$ 行驶的路程总数与小 $B$ 行驶的路程总数的比值都最小,但是城市 $2$ 的海拔更高,所以输出第一行为$2$。
【数据范围】
对于$30$%的数据,有$1≤N≤20,1≤M≤20$;
对于$40$%的数据,有$1≤N≤100,1≤M≤100$;
对于$50$%的数据,有$1≤N≤100,1≤M≤1,000$;
对于$70$%的数据,有$1≤N≤1,000,1≤M≤10,000$;
对于$100$%的数据,有$1≤N≤100,000, 1≤M≤10,000$,
$-1,000,000,000≤H_i≤1,000,000,000,0≤X_0≤1,000,000,000,1≤S_i≤N,0≤X_i≤1,000,000,000$,数据保证$H_i$互不相同。