| 题目名称 | 22. [HAOI 2005]路由选择问题 |
|---|---|
| 输入输出 | route.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 3 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:352, 提交:567, 通过率:62.08% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.17 MiB | Pascal |
| 本题关联比赛 | |||
| 4043级NOIP2022欢乐赛4th | |||
| 关于 路由选择问题 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
次短路的一个点只能经过一次么 ?
2018-11-19 20:31
17楼
| ||||
|
竟然图是个简单路,而题目木有说。
2017-08-22 15:49
16楼
| ||||
|
额,这人要是犯起二来……
有一个地方的起点不小心定义成1了……智硬了 话说不能迂回咋处理??算了蒟蒻我还是默默打个表…… | ||||
|
一开始自作聪明,以为删除最短路上的某条边,进行完相应一次求最短路之后,只把之前删除修改回去就行了。。。结果发现必须每次都从原来的图上修改才能过
顺便,main函数内外都定义了n,结果浪费半个小时在这种错误上。。。 | ||||
|
楼上三个傻x,嘿嘿嘿嘿嘿。。。。。。。。。。打表都不会了
| ||||
|
为什么不能迂回? 所以。。。。。。嘿嘿嘿嘿。。。。。。
2015-07-29 12:12
12楼
| ||||
|
不能迂回,所以,。。。。。嘿嘿嘿嘿。。。。。。
| ||||
|
我怀疑数据有误,所以......嘿嘿嘿嘿。。。。。。
| ||||
|
懒的再打一遍dijstra就粘了之前的... 结果自定义函数内变量和全局变量命名一样没注意 调试了半个多小时.... 告诫我们粘的时候要注意
2015-04-14 20:13
9楼
| ||||
|
为什么次短路不能迂回= =那还能叫次短路吗= =!
……那叫不能迂回的次短路…… | ||||
【题目描述】
$X$ 城有一个含有 $N$ 个节点的通信网络,在通信中,我们往往关心信息从一个节点 $I$ 传输到节点 $J$ 的最短路径。遗憾的是,由于种种原因,线路中总有一些节点会出故障,因此在传输中要避开故障节点。
任务一:在己知故障节点的情况下,求避开这些故障节点,从节点 $I$ 到节点 $J$ 的最短路径 $S_0$。
任务二:在不考虑故障节点的情况下,求从节点 $I$ 到节点 $J$ 的最短路径$S_1$、第二最短路径$S_2$。
所求路径均为简单路径:路径上的各顶点互不重复。
【输入格式】
第 $1$ 行: $N$ $I$ $J$ (分别表示节点个数、起始节点和目标节点)
第$2 \sim N+1$行: $S_{k_1}$ $S_{k_2}…S_{k_N}$
(表示节点 $K$ 到节点 $J$ 的距离为整数 $S_{k_J}$,若 $S_{k_j}=0$ 表示节点 $K$ 到节点 $J$ 没线路, $K=1,2,……,N$)
最后一行: $P$ $T_1$ $T_2$……$T_p$ (表示故障节点的个数及编号)
【输出格式】
$S_0$ $S_1$ $S_2$ ($S_1 \leq S_2$ 从节点 $I$ 到节点 $J$ 至少有两条不同路径)
【样例输入】
5 1 5 0 10 5 0 0 10 0 0 6 20 5 0 0 30 35 0 6 30 0 6 0 20 35 6 0 1 2
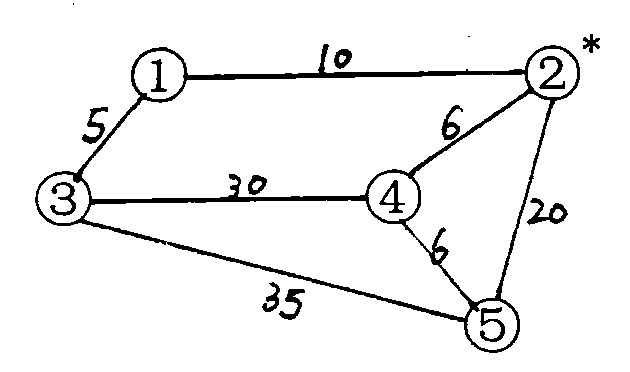
【样例输出】
40 22 30
【数据规模与约定】
对于 $100\%$ 的数据,$N \leq 50 ,S_{k_j} \leq 100 ,P \leq 5$。