| 题目名称 | 15. [NOI 2007]社交网络 |
|---|---|
| 输入输出 | network1.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:184, 提交:505, 通过率:36.44% | ||||
|
|
100 | 0.003 s | 0.59 MiB | C++ |
|
|
100 | 0.006 s | 0.31 MiB | C++ |
|
|
100 | 0.015 s | 0.45 MiB | C++ |
|
|
100 | 0.017 s | 0.18 MiB | C++ |
|
|
100 | 0.017 s | 1.36 MiB | C++ |
|
|
100 | 0.019 s | 0.50 MiB | C++ |
|
|
100 | 0.020 s | 0.50 MiB | C++ |
|
|
100 | 0.021 s | 0.45 MiB | C++ |
|
|
100 | 0.023 s | 0.38 MiB | C++ |
|
|
100 | 0.029 s | 2.96 MiB | C++ |
| 关于 社交网络 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
回复 @He :
真会爆掉。。。
2017-08-14 10:19
21楼
| ||||
|
所以说为什么直接用int不行。。
难不成是爆掉了。。 | ||||
|
| ||||
|
我SPFA求最短路个数姿势有问题?。。。。。
| ||||
|
a的第一道noi
加油加油加油      | ||||
|
注意开longlong 否则最后一个点会炸的很有趣……
话说精度爆了会输出一些有趣的东西~~!尤其是用cout的时候,很人性化哦!! 
2016-11-02 20:50
16楼
| ||||
|
出门右转双倍经验
2016-10-05 08:15
15楼
| ||||
|
目测我这是第一份SPFA->_->
| ||||
|
回复 @超级傲娇的AC酱 :
我也这么觉得
2016-07-10 10:47
13楼
| ||||
|
...
2015-10-03 20:59
12楼
| ||||
- 50%的数据中:$n ≤10,m ≤45$
- 100%的数据中:$n ≤100,m ≤4 500$,任意一条边的权值c是正整数,满足:$1 ≤c ≤1 000$
- 所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过$10^{10}$。
【问题描述】
在社交网络$(social$ $network)$的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有$n$个人,人与人之间有不同程度的关系。我们将这个关系网络对应到一个$n$个结点的无向图上,两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值$c$,$c$越小,表示两个人之间的关系越密切。
我们可以用对应结点之间的最短路长度来衡量两个人$s$和$t$之间的关系密切程度,注意到最短路径上的其他结点为$s$和$t$的联系提供了某种便利,即这些结点对于$s$和$t$之间的联系有一定的重要程度。我们可以通过统计经过一个结点$v$的最短路径的数目来衡量该结点在社交网络中的重要程度。
考虑到两个结点$A$和$B$之间可能会有多条最短路径。我们修改重要程度的定义如下:
令$C_{s,t}$表示从s到t的不同的最短路的数目,$C_{s,t}(v)$表示经过v从s到t的最短路的数目;则定义
\[ I(v) = \sum_{s \ne v, t \ne v}{\frac{C_{s,t}(v)}{C_{s,t}}} \]
为结点v在社交网络中的重要程度。
为了使$I(v)$和$C_{s,t}(v)$有意义,我们规定需要处理的社交网络都是连通的无向图,即任意两个结点之间都有一条有限长度的最短路径。
现在给出这样一幅描述社交网络$s$的加权无向图,请你求出每一个结点的重要程度。
【输入格式】
输入文件中第一行有两个整数,$n$和$m$,表示社交网络中结点和无向边的数目。在无向图中,我们将所有结点从$1$到$n$进行编号。
接下来$m$行,每行用三个整数$a, b, c$描述一条连接结点$a$和$b$,权值为$c$的无向边。注意任意两个结点之间最多有一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。
【输出格式】
输出文件包括$n$行,每行一个实数,精确到小数点后$3$位。第$i$行的实数表示结点$i$在社交网络中的重要程度。
【样例输入】
4 4 1 2 1 2 3 1 3 4 1 4 1 1
【样例输出】
1.000 1.000 1.000 1.000
【样例说明】
社交网络如下图所示。
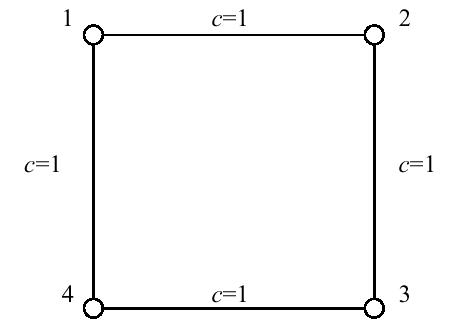
对于1号结点而言,只有2号到4号结点和4号到2号结点的最短路经过1号结点,而2号结点和4号结点之间的最短路又有2条。因而根据定义,1号结点的重要程度计算为$1/2+1/2=1$。由于图的对称性,其他三个结点的重要程度也都是1。
【评分方法】
本题没有部分分,仅当你的程序计算得出的各个结点的重要程度与标准输出相差不超过0.001时,才能得到测试点的满分,否则不得分。