| 题目名称 | 761. [CodoJam2012] 镜子大厅 |
|---|---|
| 输入输出 | 2012d.in/out |
| 难度等级 | ★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 2 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 0.904 s | 0.33 MiB | C++ |
| 本题关联比赛 | |||
| 2012 资格赛 | |||
| 关于 镜子大厅 的近10条评论(全部评论) |
|---|
Problem
You live in a 2-dimensional plane, and one of your favourite places to visit is the Hall of Mirrors. The Hall of Mirrors is a room (a 2-dimensional room, of course) that is laid out in a grid. Every square on the grid contains either a square mirror, empty space, or you. You have width 0 and height 0, and you are located in the exact centre of your grid square.
Despite being very small, you can see your reflection when it is reflected back to you exactly. For example, consider the following layout, where '#' indicates a square mirror that completely fills its square, '.' indicates empty space, and the capital letter 'X'indicates you are in the center of that square:
###### #..X.# #.#..# #...## ######
Unfortunately in the Hall of Mirrors it is very foggy, so you can't see further than D units away. Suppose D=3. If you look up, your reflection will be 1 unit away (0.5 to the mirror, and 0.5 back). If you look right, your reflection will be 3 units away (1.5 to the mirror, and 1.5 back), and you will be able to see it. If you look down, your reflection will be 5 units away and you won't be able to see it.
It's important to understand how light travels in the Hall of Mirrors. Light travels in a straight line until it hits a mirror. If light hits any part of a mirror but its corner, it will be reflected in the normal way: it will bounce off with an angle of reflection equal to the angle of incidence. If, on the other hand, the light would touch the corner of a mirror, the situation is more complicated. The following diagrams explain the cases:
In the following cases, light approaches a corner and is reflected, changing its direction:
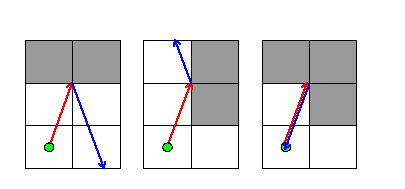
In the first two cases, light approached two adjacent mirrors at the point where they met. Light was reflected in the same way as if it had hit the middle of a long mirror. In the third case, light approached the corners of three adjacent mirrors, and returned in exactly the direction it came from.
In the following cases, light approaches the corners of one or more mirrors, but does not bounce, and instead continues in the same direction:
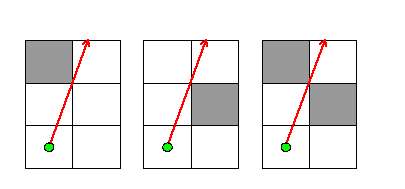
This happens when light reaches distance 0 from the corner of a mirror, but would not have to pass through the mirror in order to continue in the same direction. In this way, a ray of light can pass between two mirrors that are diagonally adjacent to each other -- effectively going through a space of size 0. Good thing it's of size 0 too, so it fits!
In the final case, light approaches the corner of one mirror and is destroyed:
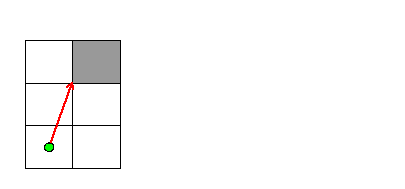
The mirror was in the path of the light, and the ray of light didn't approach the corners of any other mirrors.
Note that light stops when it hits you, but it has to hit the exact centre of your grid square.
How many images of yourself can you see?
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line containing three space-separated integers, H, W and D. H lines follow, and each contains W characters. The characters constitute a map of the Hall of Mirrors for that test case, as described above.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of reflections of yourself you can see.
Limits
1 ≤ T ≤ 100.
3 ≤ H, W ≤ 30.
1 ≤ D ≤ 50.
All characters in each map will be '#', '.', or 'X'.
Exactly one character in each map will be 'X'.
The first row, the last row, the first column and the last column of each map will be entirely filled with '#' characters.
Small dataset
There will be no more than 2W+2H-4 '#' characters.
Large dataset
The restriction from the Small dataset does not apply.
Sample
|
Input |
Output |
|
6 3 3 1 ### #X# ### 3 3 2 ### #X# ### 4 3 8 ### #X# #.# ### 7 7 4 ####### #.....# #.....# #..X..# #....## #.....# ####### 5 6 3 ###### #..X.# #.#..# #...## ###### 5 6 10 ###### #..X.# #.#..# #...## ###### |
Case #1: 4 Case #2: 8 Case #3: 68 Case #4: 0 Case #5: 2 Case #6: 28 |