本题关联比赛
SBOI虎年首秀

关于最小路径覆盖问题的近10条评论(全部评论)
复习一波二分图 Shirry 2018-04-20 21:45 17楼
为什么我建出来的图这么鬼畜，输出路径的时候有一个单点，debug了一上午胡嘉兴 2018-03-09 21:05 16楼
回复 @cstdio : hungry而不是hungary ，ε=(´ο｀*)))唉，文化课啊还有这题的spj是假的吧，洛谷可过落痕 2018-01-23 10:15 15楼
这题有special judge的不用拘泥于顺序 nonamenotitle 2017-03-22 00:14 14楼
回复 @甘罗 : sdf zkx06111 2017-02-02 08:29 13楼
Sap又短又快，赞~ 甘罗 2016-10-26 21:12 12楼
可恶的回车 ‎MistyEye 2016-06-13 17:49 11楼
哒哒哒哒哒！ 2016-06-13 17:43 10楼
WA了插件何在 0 2015-07-27 19:49 9楼
输出最后一行要打换行，否则会错。。。。。。。 mikumikumi 2015-05-18 20:13 8楼

728. [网络流24题] 最小路径覆盖问题

★★★☆ 输入文件：path3.in 输出文件：path3.out 评测插件
时间限制：1 s 内存限制：128 MiB

给定有向图$G=(V,E)$。设$P$是$G$的一个简单路（顶点不相交）的集合。如果$V$中每个顶点恰好在$P$的一条路上，则称$P$是$G$的一个路径覆盖。$P$中路径可以从$V$的任何一个顶点开始，长度也是任意的，特别地，可以为$0$。$G$的最小路径覆盖是$G$的所含路径条数最少的路径覆盖。

设计一个有效算法求一个有向无环图$G$的最小路径覆盖。

设$V={1，2，... ，n}$，构造网络$G_1$=$(V_1,E_1)$如下：

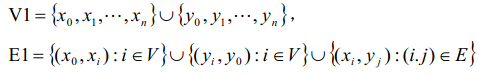
每条边的容量均为$1$。求网络$G_1$的$(x_0,y_0)$最大流。

第$1$行有$2$个正整数$n$和$m$。$n$是给定有向无环图$G$的顶点数，$m$是$G$的边数。

接下来的$m$行，每行有$2$个正整数$i$和$j$，表示一条有向边$(i,j)$。

从第$1$行开始，每行输出一条路径。文件的最后一行是最少路径数。

1 4 7 10 11
2 5 8
3 6 9
3

$1<=n<=150,1<=m<=6000$；

算法实现题$8-3$ 最小路径覆盖问题（习题$8-13$）