| 题目名称 | 547. [HAOI 2011]防线修建 |
|---|---|
| 输入输出 | defense.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:98, 提交:232, 通过率:42.24% | ||||
|
|
100 | 0.150 s | 4.26 MiB | C++ |
|
|
100 | 0.195 s | 5.73 MiB | C++ |
|
|
100 | 0.199 s | 5.85 MiB | C++ |
|
|
100 | 0.211 s | 5.08 MiB | C++ |
|
|
100 | 0.211 s | 7.47 MiB | C++ |
|
|
100 | 0.221 s | 5.65 MiB | C++ |
|
|
100 | 0.225 s | 6.61 MiB | C++ |
|
|
100 | 0.225 s | 8.07 MiB | C++ |
|
|
100 | 0.231 s | 9.65 MiB | C++ |
|
|
100 | 0.234 s | 5.08 MiB | C++ |
| 关于 防线修建 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
叉积写错花了两天时间才看出来,我的zz身份稳了
| ||||
|
回复 @呵呵酵母菌 :
可是你的数据不合法,横坐标小于n
2018-09-20 22:21
13楼
| ||||
|
5 4 2
3 5 1 5 5 4 4 4 1 1 2 1 3 2 12.07 12.07 好多代码都跑不过……
2018-03-05 09:22
12楼
| ||||
|
包子快要辣死了然而1A开心
2017-08-04 18:52
11楼
| ||||
|
手抖发两层
2017-02-27 16:01
10楼
| ||||
|
| ||||
|
并不知道哪里的变量名之类出了锅...bzoj过了,在这儿就是过不去....
| ||||
|
STL的东西一定不能打&运算符
| ||||
|
| ||||
|
摸一发,一发入魂
2016-04-11 19:49
5楼
| ||||
【题目描述】
近来 $A$ 国和 $B$ 国的矛盾激化,为了预防不测,$A$ 国准备修建一条长长的防线,当然修建防线的话,肯定要把需要保护的城市修在防线内部了。
可是 $A$ 国上层现在还犹豫不决,到底该把哪些城市作为保护对象呢?又由于 $A$ 国的经费有限,所以希望你能帮忙完成如下的一个任务:
$1$、给出你所有的 $A$ 国城市坐标;
$2$、$A$国上层经过讨论,考虑到经济问题,决定取消对 $u$ 城市的保护,也就是说 $u$ 城市不需要在防线内了;
$3$、$A$国上层询问对于剩下要保护的城市,修建防线的总经费最少是多少;
你需要对每次询问作出回答。注意单位长度的防线花费为 $1$。
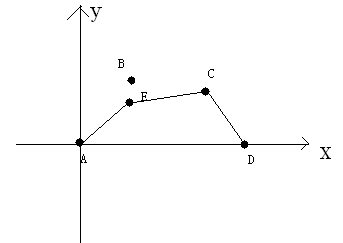
$A$ 国的地形是这样的,形如下图,$x$ 轴是一条河流,相当于一条天然防线,不需要你再修建。

$A$ 国总是有两个城市在河边,一个点是 $(0,0)$,一个点是 $(n,0)$,其余所有点的横坐标均在 $(0,n)$ 范围内,纵坐标均大于 $0$。$A$国有一个不在 $(0,0)$ 和 $(n,0)$ 的首都,$(0,0),(n,0)$ 和首都这三个城市是一定需要保护的。
上图中,$A,B,C,D,E$ 点为 $A$ 国城市,且目前都要保护,那么修建的防线就会是 $A-B-C-D$,花费也就是线段 $AB$ 的长度 $+$ 线段 $BC$ 的长度 $+$ 线段 $CD$ 的长度,如果,这个时候撤销 $B$ 点的保护,那么防线变成下图
【输入格式】
第一行三个整数 $n,x,y$ 分别表示河边城市和首都是 $(0,0),(n,0),(x,y)$。
第二行一个整数 $m$。
接下来 $m$ 行,每行两个整数 $a,b$ 表示 $A$ 国的一个非首都非河边城市的坐标为 $(a,b)$。
再接下来一个整数 $q$,表示修改和询问总数。
接下来 $q$ 行每行要么形如 $1$ $u$,要么形如 $2$,分别表示撤销第 $u$ 个城市的保护和询问。
【输出格式】
对于每个询问输出一行一个实数 $v$,表示修建防线的花费,保留两位小数。
【样例输入】
4 2 1 2 1 2 3 2 5 2 1 1 2 1 2 2
【样例输出】
6.47 5.84 4.47
【数据规模与约定】
对于 $30\%$ 的数据,$1\le m,q \le 1000$;
对于 $100\%$ 的数据,$1\le m \le 10^5$,$1\le q \le 2 \times 10^5$,$1 < n \le 10^4$。
所有点的坐标范围均在 $10^4$ 以内, 数据保证没有重点。