| 题目名称 | 341. [NOI 2005]聪聪与可可 |
|---|---|
| 输入输出 | cchkk.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:109, 提交:246, 通过率:44.31% | ||||
|
|
100 | 0.048 s | 4.57 MiB | C++ |
|
|
100 | 0.056 s | 4.54 MiB | C++ |
|
|
100 | 0.056 s | 4.76 MiB | C++ |
|
|
100 | 0.059 s | 6.37 MiB | C++ |
|
|
100 | 0.079 s | 12.03 MiB | C++ |
|
|
100 | 0.081 s | 11.80 MiB | C++ |
|
|
100 | 0.082 s | 12.99 MiB | C++ |
|
|
100 | 0.084 s | 12.99 MiB | C++ |
|
|
100 | 0.085 s | 15.13 MiB | C++ |
|
|
100 | 0.088 s | 23.68 MiB | C++ |
| 关于 聪聪与可可 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
| ||||
|
md 犯下了和 祖国栋梁 同样的错误
请各位注意 题面有毒 请谨慎食用 | ||||
|
有毒……
请问: if(!tmp)tmp=u; d[x][u]=tmp; 和 d[x][u]=tmp; if(!tmp)d[x][u]=u; 的区别是什么?前一份E,后一份AC
2017-11-06 19:12
14楼
| ||||
|
签个到证明我还活着
2017-10-21 19:54
13楼
| ||||
|
以为是连走两步最小编号的点www不过这样也有80分2333
2017-09-04 14:32
12楼
| ||||
|
概率留念
| ||||
|
2017-07-15 11:07
10楼
| ||||
|
回复 @cstdio :
改成记忆化搜索+边表之后,还是入字典序的坑了。
2016-12-24 21:48
9楼
| ||||
|
600题留念(这也是真的智障,WA4次...看错一次题- -)
2016-12-24 21:48
8楼
| ||||
|
看错了,以为n<=50,直接一发floyd+bfs就上去了,真是智障。
| ||||
- 第 $1$ 行为两个整数 $N$ 和 $E$,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。
- 第 $2$ 行包含两个整数 $C$ 和 $M$,以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。
- 接下来 $E$ 行,每行两个整数,第 $i+2$ 行的两个整数 $A_i$ 和 $B_i$ 表示景点 $A_i$ 和景点 $B_i$ 之间有一条路。
- 所有的路都是无向的,即:如果能从 $A$ 走到 $B$,就可以从 $B$ 走到 $A$。
- 输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。
- 输出 $1$ 个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉。
- 对于所有的数据,$1 ≤ N, E ≤ 1000$。
- 对于 $50\%$ 的数据,$1 ≤ N ≤ 50$。
【问题描述】
在一个魔法森林里,住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。虽然灰姑娘非常喜欢她们俩,但是,聪聪终究是一只猫,而可可终究是一只老鼠,同样不变的是,聪聪成天想着要吃掉可可。
一天,聪聪意外得到了一台非常有用的机器,据说是叫 $GPS$,对可可能准确的定位。有了这台机器,聪聪要吃可可就易如反掌了。于是,聪聪准备 马上出发,去找可可。而可怜的可可还不知道大难即将临头,仍在森林里无忧无虑的玩耍。小兔子乖乖听到这件事,马上向灰姑娘报告。灰姑娘决定尽快阻止聪聪, 拯救可可,可她不知道还有没有足够的时间。
整个森林可以认为是一个无向图,图中有 $N$ 个美丽的景点,景点从 $1$ 至 $N$ 编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。
当聪聪得到 $GPS$ 时,可可正在景点 $M(M ≤ N)$ 处。以后的每个时间单位,可可都会选择去相邻的景点(可能有多个)中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有 $P$ 个景点与景点 $M$ 相邻,它们分别是景点 $R$、景点 $S$,……景点 $Q$,在时刻 $T$ 可可处在景点 $M$,则在 $(T+1)$ 时刻,可可有 $1/(P+1)$ 的可能在景点 $R$,有 $1/(P+1)$ 的可能在景点 $S$,……,有 $1/(P+1)$ 的可能在景点 $Q$,还有 $1/(P+1)$ 的可能停在景点 $M$。
我们知道,聪聪是很聪明的,所以,当她在景点 $C$ 时,她会选一个更靠近可可的景点,如果这样的景点有多个,她会选一个标号最小的景点。由于聪聪太想吃掉可可了,如果走完第一步以后仍然没吃到可可,她还可以在本段时间内再向可可走近一步。
在每个时间单位,假设聪聪先走,可可后走。在某一时刻,若聪聪和可可位于同一个景点,则可怜的可可就被吃掉了。灰姑娘想知道,平均情况下,聪聪几步就可能吃到可可。而你需要帮助灰姑娘尽快的找到答案。
【输入格式】
【输出格式】
【样例输入1】
4 3 1 4 1 2 2 3 3 4
【样例输出1】
1.500
【样例说明1】
开始时,聪聪和可可分别在景点 $1$ 和景点 $4$。
第一个时刻,聪聪先走,她向更靠近可可(景点 $4$)的景点走动,走到景点 $2$,然后走到景点 $3$;假定忽略走路所花时间。
可可后走,有两种可能:
第一种是走到景点 $3$,这样聪聪和可可到达同一个景点,可可被吃掉,步数为 $1$,概率为 $0.5$。 第二种是停在景点 $4$,不被吃掉。概率为 $0.5$。
到第二个时刻,聪聪向更靠近可可(景点 $4$)的景点走动,只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。
所以平均的步数是 $1 * 0.5 + 2 * 0.5 = 1.5$ 步。
【样例输入2】
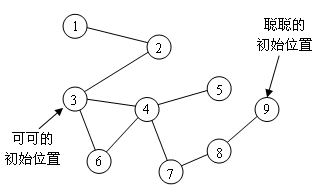
9 9 9 3 1 2 2 3 3 4 4 5 3 6 4 6 4 7 7 8 8 9
【样例输出2】
2.167
【样例说明2】
森林如下图所示: