| 题目名称 | 118. [NOIP 2006]作业调度方案 |
|---|---|
| 输入输出 | jsp.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:107, 提交:202, 通过率:52.97% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.002 s | 0.15 MiB | Pascal |
|
|
100 | 0.002 s | 0.26 MiB | C++ |
|
|
100 | 0.002 s | 0.35 MiB | C++ |
|
|
100 | 0.002 s | 0.36 MiB | C++ |
|
|
100 | 0.002 s | 0.37 MiB | C++ |
|
|
100 | 0.002 s | 0.39 MiB | C++ |
|
|
100 | 0.002 s | 0.39 MiB | C++ |
|
|
100 | 0.002 s | 0.48 MiB | C++ |
| 关于 作业调度方案 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
两星的题,一星半的语文理解,没想到2006竟也有和儒略日一样EX的题,真是为NOIP为数不多的毒瘤题之一
| ||||
|
终于过了,开始每个工序必须要求之前的工序已经完成,这里弄了个大坑……
| ||||
|
考前只想写模拟..
| ||||
|
语文很重要,简单模拟
| ||||
|
这是模拟吗?
2016-11-16 19:04
6楼
| ||||
|
| ||||
|
模拟 0 0
| ||||
|
水题居然W了(囧)
2015-06-28 20:24
3楼
| ||||
|
果然是语文课上课时看算法书的后果。
愣是看了BYvoid大神的题解后才看懂的题意。 表示确实简单,但题目描述太绕。
2014-10-09 08:17
2楼
| ||||
|
事实证明学好语文很重要- -。
2012-10-30 10:43
1楼
| ||||
【问题描述】
我们现在要利用 m 台机器加工 n 个工件,每个工件都有 m 道工序,每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。
每个工件的每个工序称为一个操作,我们用记号 j-k 表示一个操作,其中 j 为 1 到 n 中的某个数字,为工件号; k 为 1 到 m 中的某个数字,为工序号,例如 2-4 表示第 2 个工件第 4 道工序的这个操作。在本题中,我们还给定对于各操作的一个安排顺序。
例如,当 n=3 , m=2 时,“ 1-1 , 1-2 , 2-1 , 3-1 , 3-2 , 2 -2 ” 就是一个给定的安排顺序,即先安排第 1 个工件的第 1 个工序,再安排第 1 个工件的第 2 个工序,然后再安排第 2 个工件的第 1 个工序,等等。
一方面,每个操作的安排都要满足以下的两个约束条件。
(1) 对同一个工件,每道工序必须在它前面的工序完成后才能开始;
(2) 同一时刻每一台机器至多只能加工一个工件。
另一方面,在安排后面的操作时,不能改动前面已安排的操作的工作状态。
由于同一工件都是按工序的顺序安排的,因此,只按原顺序给出工件号,仍可得到同样的安排顺序,于是,在输入数据中,我们将这个安排顺序简写为“ 1 1 2 3 3 2 ” 。
还要注意,“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时,有可能排在后面的某个操作比前面的某个操作先完成。
例如,取 n=3,m=2 ,已知数据如下:
|
工件号 |
机器号 / 加工时间 |
|
|
工序 1 |
工序 2 |
|
|
1 |
1/3 |
2/2 |
|
2 |
1/2 |
2/5 |
|
3 |
2/2 |
1/4 |
则对于安排顺序“ 1 1 2 3 3 2 ” ,下图中的 两个实施方案都是正确的。但所需要的总时间分别是 10 与 12 。
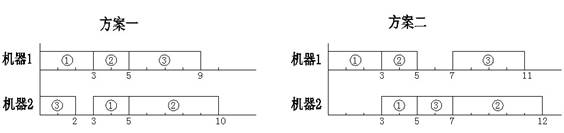
当 一个操作插入到某台机器的某个空档时(机器上最后的尚未安排操作的部分也可以看作一个空档),可以靠前插入,也可以靠后或居中插入。为了使问题简单一些, 我们约定:在保证约束条件(1)(2)的条件下,尽量靠前插入。并且,我们还约定,如果有多个空档可以插入,就在保证约束条件(1)(2)的条件下,插入到最前面的一个空档。于是,在这些约定下,上例中的方案一是正确的,而方案二是不正确的。
显然,在这些约定下,对于给定的安排顺序,符合该安排顺序的实施方案是唯一的,请你计算出该方案完成全部任务所需的总时间。
【输入格式】
第 1 行为两个正整数,用一个空格隔开:m n(其中m(<20)表示机器数,n(<20)表示工件数)
第 2 行: m*n个用空格隔开的数,为给定的安排顺序。
接下来的 2n 行,每行都是用空格隔开的 m 个正整数,每个数不超过 20 。
其中前 n 行依次表示每个工件的每个工序所使用的机器号,第 1 个数为第 1 个工序的机器号,第 2 个数为第 2 个工序机器号,等等。
后 n 行依次表示每个工件的每个工序的加工时间。
可以保证,以上各数据都是正确的,不必检验。
【输出格式】
输出只有一个正整数,为最少的加工时间。
【输入样例】
2 3 1 1 2 3 3 2 1 2 1 2 2 1 3 2 2 5 2 4
【输出样例】
10