| 题目名称 | 434. 可怜的蜘蛛 |
|---|---|
| 输入输出 | spider.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:14, 通过率:7.14% | ||||
|
|
100 | 0.003 s | 0.31 MiB | C++ |
|
|
90 | 0.003 s | 0.31 MiB | C++ |
|
|
90 | 0.003 s | 0.31 MiB | C++ |
|
|
80 | 0.003 s | 0.31 MiB | C++ |
|
|
80 | 0.003 s | 0.31 MiB | C++ |
|
|
70 | 0.003 s | 0.31 MiB | C++ |
|
|
70 | 0.012 s | 0.31 MiB | C++ |
|
|
30 | 0.002 s | 0.31 MiB | C++ |
|
|
10 | 0.001 s | 0.31 MiB | C++ |
|
|
10 | 0.003 s | 0.31 MiB | C++ |
| 本题关联比赛 | |||
| 20100421 | |||
| 关于 可怜的蜘蛛 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
2013-02-08 20:07
2楼
| ||||
|
尼玛没办法只能cheat了……淡淡的忧桑……
这道题……目测有90%的编程复杂度都是用来解……决……边……界……问……题……的……代码写的像shit一样……
2013-02-07 20:36
1楼
| ||||
【问题描述】
蛛蛛William经常居住在Petro博士的化学实验室里面。悠闲的William常常漫步于实验室的管道上,甚至有时还会光顾一下里面空空的管道。一天晚上,它逛得实在太累了,居然在管道中睡着了。第二天早上,Petro士来到实验室,打开阀门往管道里注入热水,准备新一天的实验研究工作。就在这千钧一发的时刻,William的好朋友小灰鼠Stanley意识到问题的严重性,拼命地往阀门跑去。然而Stanley的努力还是无法挽回好朋友william的生命。
可怜的蜘蛛William被烫死了,留给Stanley只有痛苦的回忆。虽然Stanley尽了自己最大的努力,但它内心还是感觉很内疚。它想知道从Petro博士打开阀门那一刻开始,它有多少时间去拯救好朋友。它的心情是如此的差,以至于无法自己计算。你能帮助它吗?
所有的管道都是直径1cm垂直放置的底部封闭开口向上的圆柱体。有些管道之间有水平的小细管相连。由于直径很细,任何时候流动在小细管中的水的体积可以忽略不计。水从一个管道上方以恒定的速度0.25picm3/s注入。管道中的水越来越多,当水位到达跟某管道相连的小细管时,该管道也开始注入水。根据基本的物理原理,我们知道对于两个相连的管道,如果水位已经超过连接它们的小细管,往其中任意一个管道注水,两个管道的水位都会保持一致。在这种情况下,其中一个管道的水增量只有注入水总量的二分之一。
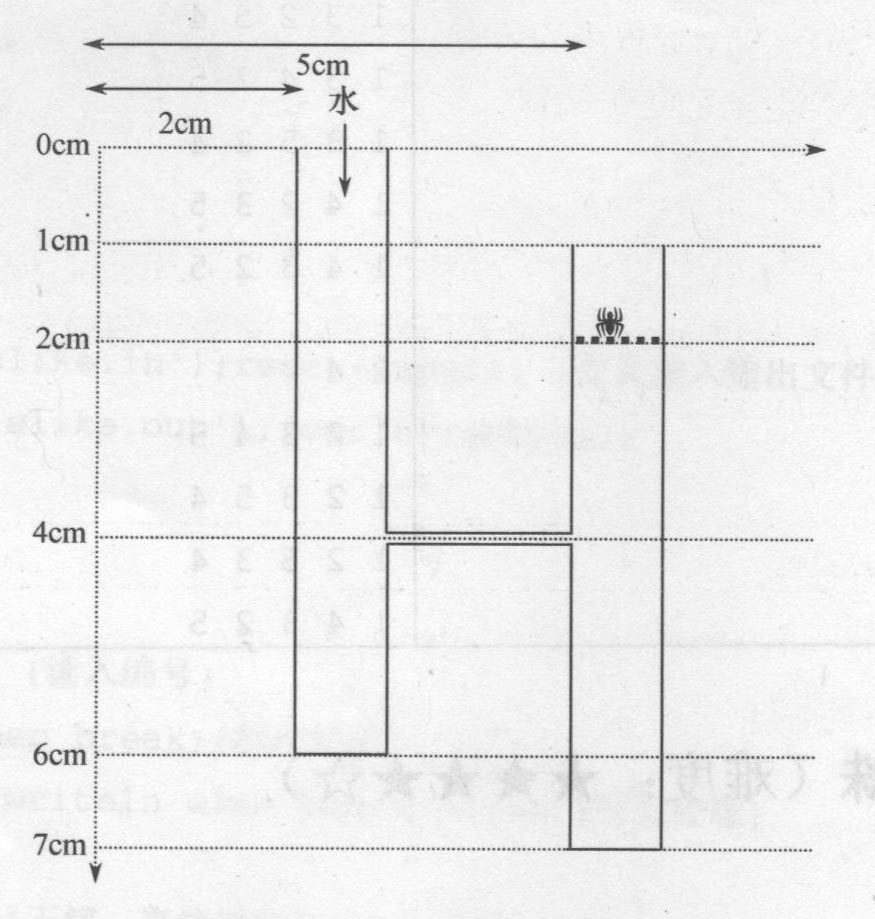
例如,对于如图所示情况:
可怜的蜘蛛William被烫死了,留给Stanley只有痛苦的回忆。虽然Stanley尽了自己最大的努力,但它内心还是感觉很内疚。它想知道从Petro博士打开阀门那一刻开始,它有多少时间去拯救好朋友。它的心情是如此的差,以至于无法自己计算。你能帮助它吗?
所有的管道都是直径1cm垂直放置的底部封闭开口向上的圆柱体。有些管道之间有水平的小细管相连。由于直径很细,任何时候流动在小细管中的水的体积可以忽略不计。水从一个管道上方以恒定的速度0.25picm3/s注入。管道中的水越来越多,当水位到达跟某管道相连的小细管时,该管道也开始注入水。根据基本的物理原理,我们知道对于两个相连的管道,如果水位已经超过连接它们的小细管,往其中任意一个管道注水,两个管道的水位都会保持一致。在这种情况下,其中一个管道的水增量只有注入水总量的二分之一。
例如,对于如图所示情况:
首先,水以全速注入左边管道最下2cm;然后水注入右边管道最下的3cm。接着两条管道水位同时以原先速度的二分之一上升。
输入你程序的数据包含仪器中各个管道和细管的位置,以及蜘蛛所处的管道及深度。
你的程序应该返回在水淹没William,之前,Stanley有多少时间去救它的好朋友。如图所示例子的答案是9s.
你的程序应该返回在水淹没William,之前,Stanley有多少时间去救它的好朋友。如图所示例子的答案是9s.

为了简化问题,题目假设水下降速度很快,从开口下降所用的时间忽略不计。蜘蛛所在的位置可以假定为描述深度稍微高一点点的地方。比如,蜘蛛处于图1.3.1左边管道深度为4的地方的时候,那么答案应当是5,而不是2。同时,如果水到达一个管道的出口的时候,水并不会立刻溢出。只有等所有跟其相连的管道低于该开口的空间都充满了水的时候,水才开始溢出。(不排除有小细管处于开口的垂直位置的情况。)
【输入格式】
输入格式(输入文件名spider.in)
我们用管道或小细管的左上方的坐标(x,y)表示它们的位置(x轴坐标从左到右递增,y轴坐标从上到下递增)。
所有的坐标都是从0到100的整数(即O≤x≤100,0≤v≤100)。
文件的第1行是t,表示输入文件包含t个输入数据(1≤f≤10)。
对于每个输入数据:
数据的第1部分第1行是管道的数目p(1≤p≤20),接着p行分别描述各个管道。每一个管道由3个整数(x,y,h)描述,表示管道的左上角坐标(x,y)和管道的深度.h(1≤h≤20)。注意管道的直径恒为1cm。
数据的第2部分第1行是小细管的数目g(0≤g≤50),接着q行分别描述各个小细管。
每一个小细管也是由3个整数(x,y,l)描述,表示小细管的左端点坐标(x,y)和小细管的长度(1≤l≤20)。假设小细管的宽度为0。
数据的最后一行有两个整数。第1个表示William所在管道在输入数据中的序号。第2个整数表示William所处的位置(用y坐标表示)。William当时可能不在管道中(可能伤心的Stanley把William所在的位置记错了)。
可以假定:
(1)水从第一个管道注入;
(2)没有小细管会穿过管道;
(3)任意两个小细管处于不同的高度;
(4)任意两个管道的左上角坐标不同;
(5)任何小细管的端点跟管道相连。
我们用管道或小细管的左上方的坐标(x,y)表示它们的位置(x轴坐标从左到右递增,y轴坐标从上到下递增)。
所有的坐标都是从0到100的整数(即O≤x≤100,0≤v≤100)。
文件的第1行是t,表示输入文件包含t个输入数据(1≤f≤10)。
对于每个输入数据:
数据的第1部分第1行是管道的数目p(1≤p≤20),接着p行分别描述各个管道。每一个管道由3个整数(x,y,h)描述,表示管道的左上角坐标(x,y)和管道的深度.h(1≤h≤20)。注意管道的直径恒为1cm。
数据的第2部分第1行是小细管的数目g(0≤g≤50),接着q行分别描述各个小细管。
每一个小细管也是由3个整数(x,y,l)描述,表示小细管的左端点坐标(x,y)和小细管的长度(1≤l≤20)。假设小细管的宽度为0。
数据的最后一行有两个整数。第1个表示William所在管道在输入数据中的序号。第2个整数表示William所处的位置(用y坐标表示)。William当时可能不在管道中(可能伤心的Stanley把William所在的位置记错了)。
可以假定:
(1)水从第一个管道注入;
(2)没有小细管会穿过管道;
(3)任意两个小细管处于不同的高度;
(4)任意两个管道的左上角坐标不同;
(5)任何小细管的端点跟管道相连。
【输出格式】
输出格式(输出文件名spider.out)
输出文件应该包含f行输出数据,分别对应f个输入数据。如果可能的话,输出数据是一个整数,表示水到达William所在位置所用的时间,否则输出“No Solution”(这个时候水不可能到达William所在的位置)。
输出文件应该包含f行输出数据,分别对应f个输入数据。如果可能的话,输出数据是一个整数,表示水到达William所在位置所用的时间,否则输出“No Solution”(这个时候水不可能到达William所在的位置)。
【输入输出样例】
输入(spider.in)
1
输入(spider.in)
1
2
2 O 6
5 1 6
1
2 O 6
5 1 6
1
3 4 2
2 2
输出(spider.out)
9
2 2
输出(spider.out)
9