| 题目名称 | 254. [POI 2001] 交通网络图 |
|---|---|
| 输入输出 | pod.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 11 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:7, 提交:16, 通过率:43.75% | ||||
|
|
100 | 0.004 s | 0.47 MiB | C++ |
|
|
100 | 0.008 s | 0.33 MiB | C++ |
|
|
100 | 0.017 s | 0.28 MiB | C++ |
|
|
100 | 0.017 s | 0.52 MiB | C++ |
|
|
100 | 0.022 s | 0.43 MiB | C++ |
|
|
100 | 0.060 s | 1.07 MiB | C++ |
|
|
100 | 0.085 s | 25.43 MiB | C++ |
|
|
81 | 2.003 s | 0.40 MiB | C++ |
|
|
81 | 2.041 s | 0.36 MiB | C++ |
|
|
45 | 0.015 s | 0.28 MiB | C++ |
| 关于 交通网络图 的近10条评论(全部评论) |
|---|
- 从文件中读入对交通网的描述,交通路线,起始车站x,终点车站y,旅行开始的时间gx和mx(gx表示小时,mx表示分钟);
- 找出从x到y的最早到达时间;
- 把到车站y的最早时间gy:my写入文件。
- 车站总数n(1≤n≤1000);
- 路线数目k(1≤k≤2000);
- 起点车站x(1≤x≤n);
- 终点车站y(1≤y≤n);
- 旅行开始时刻中的小时gx(0≤gx≤23);
- 旅行开始时间中的分钟mx(0≤mx≤59)。
- 描述路线l的第一行是两个用一空格分开的整数:sl和cl,分别表示路线经过的车站数目和发车周期,其中2≤sl≤n,cl属于集合{6,10,15,20,30,60}。
- 描述路线l的第二行有sl个不同的整数,以一个空格分开:pl,1,pl,2,...,pl,sl,表示路线l经过车站的编号( 当1≤i≤sl时,1≤pl,i≤n)。
- 描述路线l的第三行有sl-1个用空格分开的整数:rl,1, rl,2,..., rl,sl-1,表示路线l上相邻两车站间的行驶时间,以分钟作为单位( 当1≤i≤sl-1时,1≤rl,i≤240)。
让我们先确定某个城市的交通网络图,图中的点(编号为1..n),表示车站;边(pi,pj) (其中pi≠pj),表示有一条路线直接连接车站pi和pj(1≤pi, pj≤n)。城市中的公共汽车线路从1到k编号。在线路l上有车站pl,1, pl,2,...,pl,sl,,用rl,1, rl,2,...,rl,sl-1表示对应相邻两车站间的行驶时间。例如rl,1 是从车站pl,1 到pl,2所需的时间,rl,2是从车站pl,2到pl,3所需的时间。同一线路上的车站互不相同(即若i≠j则pl,i≠pl,j)。在线路l上,发车 时间有固定的周期,表示为cl, 其中cl 属于集合{6, 10, 12, 15, 20, 30, 60};而且在每个整点g:0 (0≤g≤23),从车站pl,1 必有一辆车出发。于是可知在g:cl,、g:2cl,... 时(g:cl 表示g小时后的cl分钟),都有车出发。所有的路线均为双向:从车站pl,1到pl,sl ,从车站pl,sl 到 pl,1,且同时以车。在这样的一个城市中,我们打算做一次从车站x到车站y的旅行。你可以假定该旅行是能够完成的,而且所需的时间不超过24小时。旅行 中在任一车站我们都可以换车,上下车的时间不计,但等车的时间要计算在内。我们的目的是尽可能快地完成从车站x到车站y的旅行。
下图是一个有6个车站的交通网,有两条公共汽车线路。线路1:经过车站1、3、4、6;线路2:经过车站2、4、3、5。发车的周期是:c1=15,c2=20。相邻车站间行驶时间己标在图中的边上,以下标1、2表示不同的线路。
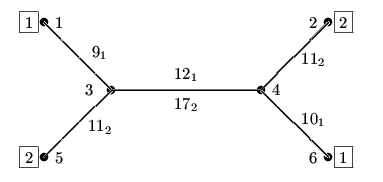
假定在23:30我们在车站5,目标是到车站6。则必须等10分钟(在23:40)才有一班2路车从车站5出发。接下来有两种旅行方案,其 一:在23:51到达车站3,等3分钟,改乘1路车到达车站6(0:16)。其二:继续乘2路车到车站4(0:8),再等13分钟(0:21)乘1路车到 车站6(0:31)。因此到达车站6时最早的时间是0:16。
任务:
输入:
文件的第一行是6个用空格分开的整数:
车站从1至n编号,路线从1至k编号。接下来的3k行用来描述路线,每条路线的描述占3行:
所有路线的车站数目之和不超过4000(即s1+s2+...+sk≤4000)。
输出:
文件中仅有两个用一空格分开的整数,即最早到达终点的时间:gy和my,(0≤gy≤23,0≤my≤59)。
输入样例:
6 2 5 6 23 30 4 15 1 3 4 6 9 12 10 4 20 5 3 4 2 11 17 11
输出样例:
0 16