题目名称	333. [NOI 2002]荒岛野人
输入输出	`savage.in/out`
难度等级	★★
时间限制	2000 ms (2 s)
内存限制	128 MiB
测试数据	10
题目来源	BYVoid 于2009-05-20加入
开放分组	全部用户
提交状态
分类标签	NOI 数学数论扩展欧几里得算法
	分享题解

通过：163，提交：410，通过率：39.76%
金身人面兽	100	0.330 s	0.12 MiB	C++
Hzoi_chairman	100	0.332 s	0.12 MiB	C++
槿柒	100	0.359 s	0.12 MiB	C++
小DOTA	100	0.366 s	0.28 MiB	C++
浮生随想	100	0.369 s	0.31 MiB	C++
洛克索耶夫	100	0.369 s	0.31 MiB	C++
Hzoi_YJX	100	0.370 s	0.31 MiB	C++
牧殇	100	0.373 s	0.31 MiB	C++
Hzoi_Queuer	100	0.382 s	0.29 MiB	C++
zmh	100	0.384 s	0.29 MiB	C++

本题关联比赛
201712练习

关于荒岛野人的近10条评论(全部评论)
只会暴力 AAAAAAAAAA 2017-10-03 11:29 8楼
我是尹鹏哲，我要带领汉子踏平这个世界！！！！！ hee 2017-10-02 18:59 7楼
我是尹鹏哲，我要带领妹子踏平这个世界！！！！！ test 2017-10-02 18:54 6楼
Cooook 2017-08-14 21:42 5楼
以下是范一隆的证明：扩展欧几里德：求ax+by=gcd(a,b)的一组解若gcd(a,b)==a 即b==0时显然 x=1，y=0 成立若gcd(a,b)!= a 即 b>0 时在欧几里德算法的基础上有 gcd(a,b)==gcd(b,a%b)则下次递归的x’ 和y’ 满足 bx’ + (a%b)y’ = gcd(b，a%b)=gcd(a，b)； a%b ==a- a/b(取整数部分) b (数学中可以用[]表示向下取整) bx’ + (a-a/bb)y’ == gcd(a,b) 将括号部分拆开得到 bx’ + ay’-(a/b) by’ == gcd(a,b) == ay’ + b(x’-a/by’) 所以x=y’ ,y=x’-a/b*y’; SOBER GOOD BOY 2016-07-12 19:30 4楼
@哒哒哒哒哒! 神啦! 洛克索耶夫 2016-07-11 21:16 3楼
安呐一条小咸鱼。 2016-07-09 15:48 2楼
神利·代目 2015-08-04 18:43 1楼

333. [NOI 2002]荒岛野人

★★ 输入文件：savage.in 输出文件：savage.out 简单对比
时间限制：2 s 内存限制：128 MiB

【问题描述】

克里特岛以野人群居而著称。岛上有排列成环行的 $M$ 个山洞。这些山洞顺时针编号为 $1,2,\dots,M$。岛上住着 $N$ 个野人，一开始依次住在山洞 $C_1,C_2,\dots,C_N$ 中，以后每年，第 $i$ 个野人会沿顺时针向前走 $P_i$ 个洞住下来。每个野人 $i$ 有一个寿命值 $L_i$，即生存的年数。下面四幅图描述了一个有 $6$ 个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为 $1,2,3$；每年要走过的洞穴数依次为 $3,7,2$；寿命值依次为 $4,3,1$。

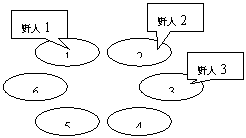
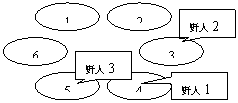
Image:Savage1.gif Image:Savage2.gif

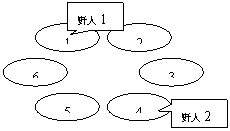
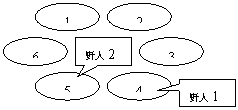
Image:Savage3.gif Image:Savage4.gif

奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

【输入文件】

输入文件的第 $1$ 行为一个整数 $N(1\le N\le 15)$，即野人的数目。第 $2$ 行到第 $N+1$ 每行为三个整数 $C_i, P_i, L_i(1\le C_i,P_i\le 100,0\le Li\le 10^6)$，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

【输出文件】

输出文件仅包含一个数 $M$，即最少可能的山洞数。输入数据保证有解，且 $M$ 不大于 $10^6$。

【样例输入】

【样例输出】

【样例说明】

该样例对应于题目描述中的例子。