| 题目名称 | 2605. [HZOI 2016] 寒假ing |
|---|---|
| 输入输出 | broken.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
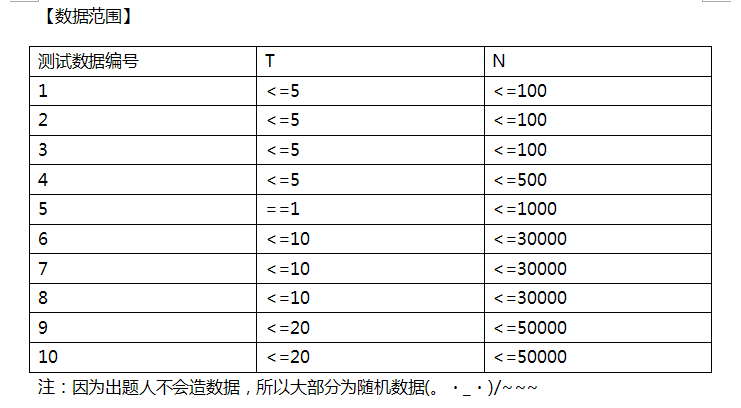
| 测试数据 | 10 |
| 题目来源 |
 _Itachi
于2017-01-25加入 |
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过：24， 提交：42， 通过率：57.14% | ||||
 6666 |
100 | 0.770 s | 5.49 MiB | C++ |
 kito |
100 | 0.832 s | 6.14 MiB | C++ |
|
_Itachi |
100 | 0.844 s | 5.68 MiB | C++ |
|
_Itachi |
100 | 0.868 s | 5.11 MiB | C++ |
|
_Itachi |
100 | 0.879 s | 5.11 MiB | C++ |
|
_Itachi |
100 | 0.890 s | 5.68 MiB | C++ |
|
_Itachi |
100 | 0.953 s | 5.68 MiB | C++ |
|
_Itachi |
100 | 0.961 s | 5.68 MiB | C++ |
 哒哒哒哒哒！ |
100 | 0.971 s | 5.52 MiB | C++ |
|
_Itachi |
100 | 1.000 s | 5.68 MiB | C++ |
| 本题关联比赛 | |||
| 寒假颓废练习 | |||
| 关于 寒假ing 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
| ||||
|
拿这道题来作为SA板子题，写了一遍又一遍
_Itachi
2017-02-12 18:59
13楼
| ||||
|
回复 @Mike is Fool :
这个。。时间复杂度分析我真的不会，只是知道倍增的大常数以及COGS老爷机害了你、、、  ONCE AGAIN
2017-01-26 15:06
12楼
| ||||
|
回复 @ONCE AGAIN :
感谢神犇的指教，但是我这种做法复杂度也是正确的啊! | ||||
|
回复 @Mike is Fool :
并没有卡常，标称极限数据0.3秒过。 正解：首先枚举长度L，一段连续重复子串一定包含了两个下标为L的倍数的字符，设这两个位置为a1,a2，首先求出k = LCP（Suffix（a1），Suffix（a2））。如果k%L！=0那么记录jj = L - k%L，再次求LCP（Suffix（a1-jj），Suffix（a2-jj）），取两者的最大值更新答案就好。 ONCE AGAIN
2017-01-26 11:01
10楼
| ||||
|
回复 @Mike is Fool :
懒得写n*反ackmann(n)的Tarjan了......再说这个做法本来不就自带一个log么...... | ||||
|
回复 @AntiLeaf :
我想我们是不是应该试试SAM+Tarjan- -这样速度应该是挺快的 | ||||
|
回复 @Mike is Fool :
我写的就是后缀自动机+ST LCA...... | ||||
|
回复 @ONCE AGAIN :
还有一点，如果不反转的话怎么求向前匹配长度呢？似乎只能求向后匹配的长度吧。 是的，我发现了，应该在开大一点，但是卡常我也是无语了，不是要我们都来SAM+Tarjan吧。难道说应该hash乱搞！？ | ||||
|
回复 @AntiLeaf :
后缀自动机，如果你不用RMQ优化O(1)求LCA，每次的复杂度可是O(nlog^2n)的，后缀树组+RMQ或者后缀自动机+RMQ复杂度应该差不多 | ||||
rewine
FoolMike
AntiLeaf
