| 题目名称 | 3290. [CSP 2019S]括号树 |
|---|---|
| 输入输出 | brackets.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:41, 提交:101, 通过率:40.59% | ||||
|
|
100 | 0.278 s | 14.41 MiB | C++ |
|
|
100 | 0.287 s | 10.81 MiB | C++ |
|
|
100 | 0.331 s | 60.82 MiB | C++ |
|
|
100 | 0.340 s | 13.60 MiB | C++ |
|
|
100 | 0.356 s | 21.37 MiB | C++ |
|
|
100 | 0.405 s | 15.73 MiB | C++ |
|
|
100 | 0.422 s | 20.80 MiB | C++ |
|
|
100 | 0.440 s | 20.93 MiB | C++ |
|
|
100 | 0.441 s | 20.42 MiB | C++ |
|
|
100 | 0.442 s | 34.01 MiB | C++ |
| 本题关联比赛 | |||
| EYOI常规赛 4th | |||
| EYOI常规赛 4th | |||
| 近5年noip/csp题目回顾 | |||
| 关于 括号树 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
什么鬼题,要加代码还要O2,,,
2019-12-17 20:50
1楼
| ||||
【题目背景】
本题中合法括号串的定义如下:
• $()$ 是合法括号串。
• 如果$ A $是合法括号串,则 $(A)$ 是合法括号串。
• 如果 $A,B$ 是合法括号串,则 $AB$ 是合法括号串。
本题中子串与不同的子串的定义如下:
字符串 $S$ 的子串是 $S$ 中连续的任意个字符组成的字符串。$S$ 的子串可用起始位置 $l$ 与终止位置 $r$ 来表示,记为 $S( l,r )( 1≤l≤r≤∣S∣$,$|S|$ 表示 $S$ 的长度)。$S$ 的两个子串视作不同当且仅当它们在 $S$ 中的位置不同,即 $l$ 不同或 $r$ 不同。
【题目描述】
一个大小为 $n$ 的树包含 $n$ 个结点和 $n−1$ 条边,每条边连接两个结点,且任意两个结点间有且仅有一条简单路径互相可达。
小 $Q$ 是一个充满好奇心的小朋友,有一天他在上学的路上碰见了一个大小为 $n$ 的树,树上结点从 $1 ∼ n$ 编号,$1$ 号结点为树的根。除 $1$ 号结点外,每个结点有一个父亲结点,$u( 2≤u≤n )$号结点的父亲为 $f_u( 1≤fu<u )$号结点。
小 $Q$ 发现这个树的每个结点上恰有一个括号,可能是$( $或 $)$。小$ Q $定义 $s_i$ 为:将根结点到 $i$ 号结点的简单路径上的括号,按结点经过顺序依次排列组成的字符串。
显然 $s_i$ 是个括号串,但不一定是合法括号串,因此现在小 $Q$ 想对所有的 $i( 1≤i≤n )$求出,$s_i$ 中有多少个互不相同的子串是合法括号串。
这个问题难倒了小$ Q$,他只好向你求助。设 $s_i$ 共有 $k_i$ 个不同子串是合法括号串, 你只需要告诉小$ Q$ 所有 $i×ki$ 的异或和,即:
$$(1×k_1) xor (2×k_2) xor (3×k_3) xor ⋯ xor (n×k_n)$$
其中 $xor$ 是位异或运算。
【输入格式】
第一行一个整数 $n$,表示树的大小。
第二行一个长为 $n$ 的由$($ 与$)$ 组成的括号串,第 $i$ 个括号表示 $i$ 号结点上的括号。
第三行包含 $n−1$ 个整数,第 $i( 1≤i<n )$个整数表示 $i+1$ 号结点的父亲编号 $f_{i+1}$。
【输出格式】
仅一行,一个整数,表示答案。
【样例输入】
5 (()() 1 1 2 2
【样例输出】
6
【样例解释】
树的形态如下图:
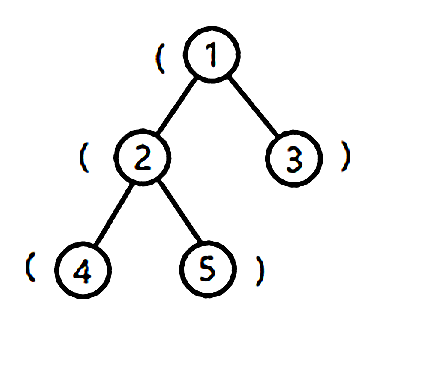
将根到 1 号结点的简单路径上的括号,按经过顺序排列所组成的字符串为 (,子串是合法括号串的个数为 0。
将根到 2 号结点的字符串为 ((,子串是合法括号串的个数为 0。
将根到 3 号结点的字符串为 (),子串是合法括号串的个数为 1。
将根到 4 号结点的字符串为 (((,子串是合法括号串的个数为 0。
将根到 5 号结点的字符串为 ((),子串是合法括号串的个数为 1。
【数据规模与约定】
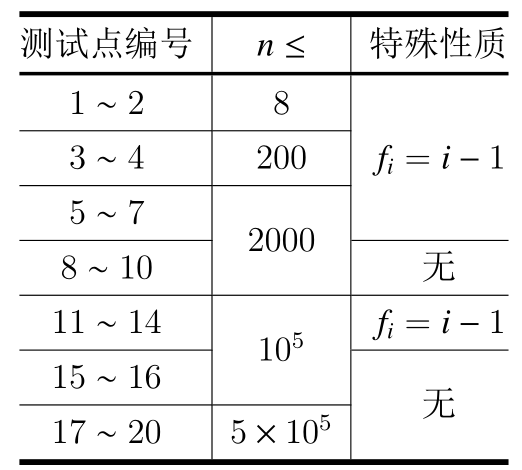
【来源】
CSP-S 2019 Day1 Task 2