| 题目名称 | 1607. [UVa 1025] 城市里的间谍 |
|---|---|
| 输入输出 | uva_1025.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 3 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:11, 提交:26, 通过率:42.31% | ||||
|
|
100 | 0.007 s | 1.15 MiB | C++ |
|
|
100 | 0.014 s | 0.41 MiB | C++ |
|
|
100 | 0.014 s | 0.42 MiB | C++ |
|
|
100 | 0.022 s | 0.46 MiB | C++ |
|
|
100 | 0.026 s | 0.42 MiB | C++ |
|
|
100 | 0.027 s | 1.33 MiB | C++ |
|
|
100 | 0.028 s | 0.44 MiB | C++ |
|
|
100 | 0.040 s | 3.36 MiB | C++ |
|
|
100 | 0.044 s | 13.86 MiB | C++ |
|
|
100 | 0.708 s | 36.55 MiB | C++ |
| 关于 城市里的间谍 的近10条评论(全部评论) |
|---|
【题目描述】
某城市的地铁是线性的,有 $n(2\le n\le 50)$ 个车站,从左到右编号为 $1~n$。有 $M_1$ 辆列车从第 $1$ 站开始往右开,还有 $M_2$ 辆列车从第 $n$ 站开始往左开。在时刻 $0$,Mario 从第 $1$ 站出发,目的是在时刻 $T(0\le T\le 200)$ 会见车站 $n$ 的一个间谍。在车站等车时容易被抓,所以她决定尽量躲在开动的火车上,让在车站等待的总时间尽量短。列车靠站停车时间忽略不计,且 Mario 身手敏捷,即使两辆方向不同的列车在同一时间靠站,Mario 也能完成换乘。(修正,数据范围内有时刻T超过200的存在,建议将数据T认为大小为500.————5801)
(提示:输入数据中包含多组数据,最后以0为输入结束的标记————5801)
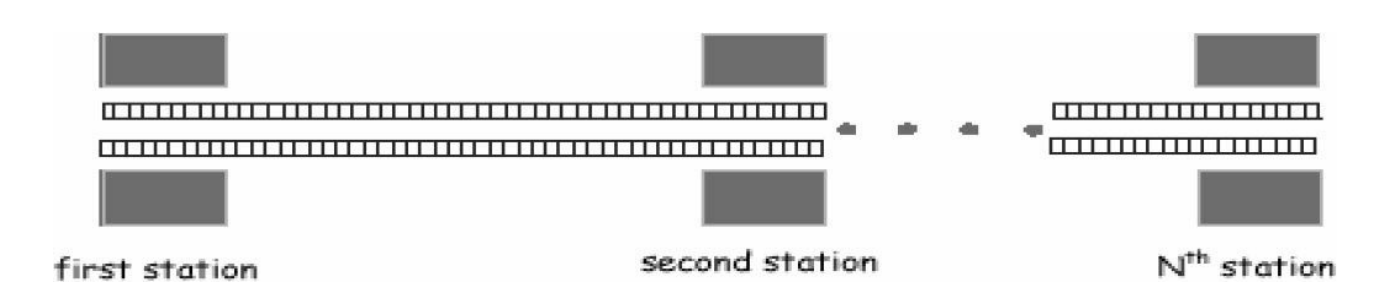
【输入格式】
输入第 $1$ 行为 $n$,第 $2$ 行为 $T$,第 $3$ 行有 $n-1$ 个整数 $t_1,t_2,\dots ,t_{n-1}(1\le t_i\le 70)$,其中 $t_i$ 表示地铁从车站 $i$ 到 $i+1$ 的行驶时间(两个方向一样)。第 $4$ 行为 $M_1(1\le M_1\le 50)$,即从第 $1$ 站出发向右开的列车数目。第 $5$ 行包含 $M_1$ 个整数 $d_1,d_2,\dots ,d_{M_1}(0\le d_i\le 250.d_i\lt d_i+1)$,即各列车的出发时间。第 $6$、$7$ 行描述从第 $n$ 站出发向左开的列车,格式同第 $4$、$5$ 行。
最后一种情况以一行0结尾。
【输出格式】
输出仅包含一行,即最少等待时间。无解输出“impossible”。
【样例输入】
4
55
5 10 15
4
0 5 10 20
4
0 5 10 15
4
18
1 2 3
5
0 3 6 10 12
6
0 3 5 7 12 15
2
30
20
1
20
7
1 3 5 7 11 13 17
0
【样例输出】
Case Number 1: 5 Case Number 2: 0 Case Number 3: impossible
【提示】
数据很弱,别抱太大希望。
【来源】
UVa 1025 A Spy in the Metro