| 题目名称 | 2136. [SGU U294]他的圆圈 |
|---|---|
| 输入输出 | Hescircle.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 5000 ms (5 s) |
| 内存限制 | 64 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:15, 提交:56, 通过率:26.79% | ||||
|
|
100 | 0.178 s | 34.02 MiB | C++ |
|
|
100 | 0.246 s | 6.78 MiB | C++ |
|
|
100 | 1.229 s | 1.55 MiB | C++ |
|
|
100 | 1.996 s | 4.87 MiB | C++ |
|
|
100 | 2.528 s | 2.60 MiB | C++ |
|
|
100 | 2.661 s | 6.21 MiB | C++ |
|
|
100 | 2.902 s | 4.10 MiB | C++ |
|
|
100 | 2.914 s | 3.69 MiB | C++ |
|
|
100 | 3.287 s | 1.81 MiB | C++ |
|
|
100 | 3.293 s | 1.84 MiB | C++ |
| 本题关联比赛 | |||
| 新春水题赛 | |||
| 关于 他的圆圈 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
第一次把范围看成2e6,于是吓得我赶紧写FFT,后来发现FFT可以过2e6的数据,但是内存得大一点……
| ||||
|
总共用时0.2s,一个点竟然给5s,我觉得有必要把时限限制得稍紧一些
 ======我是分割线===== E,X两个字母就是用两个颜色对物体染色,物体置换群G = {转0格,转1格,...,转(n-1)格},对于每一个置换 $g$,拆解得循环节个数为 $c(g)$,容易发现转 $k$格的置换$ g_{k} $ 的循环节个数 $ c(g_{k}) = gcd(k, n) $ 直接套用polya定理,最后答案就是 $ \frac{1}{n} \sum_{k=0}^{n-1} 2^{gcd(k, n)} $ 然后我这么快的高精度运算模板都还是TLE了,于是我们对于$ \frac{1}{n} $右边的式子继续进行化简 $ \sum_{i=0}^{n-1} 2^{gcd(i, n)} $ $ = \sum_{d|n}^{ } \sum_{i=1}^{n} 2^{gcd(i, n)} [gcd(i, n) == d] $ $ = \sum_{d|n}^{ } \sum_{i=1}^{n} 2^{gcd(\lfloor \frac{i}{d} \rfloor,\lfloor \frac{n}{d} \rfloor)} [gcd(\lfloor \frac{i}{d} \rfloor,\lfloor \frac{n}{d} \rfloor) == 1] $ 熟悉积性函数那套理论的同学一眼就看出了每个约数d对答案的贡献为$ 2^d \phi(\frac{n}{d})$ 最后答案就是$ \frac{1}{n} \sum_{i|n}^{ } 2^i \phi(\frac{n}{i}) $ =====我是分割线===== 压位+FFT一块使用,效果惊人  | ||||
|
这题根本目的是练习高精度......
2016-10-17 07:44
2楼
| ||||
|
由于cojs评测姬的速度比SGU慢,所以时限放到5S。
| ||||
【题目描述】
zlx在一个圆圈上写了N个字母,每个字母是'E'或'X'。他写出了所有可能的排列方式,一共2^N个,然后他发现有一些排列可以通过其他的排列通过旋转得到,他称这两个排列为本质上相同的。他现在想知道有多少种本质上不同的排列方法。
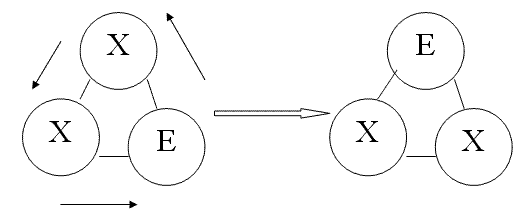
【输入格式】
一个N(1<=N<=200000).
【输出格式】
本质不同的方案的个数。
【样例输入】
4
【样例输出】
6
【提示】
在此键入。
【来源】
http://acm.sgu.ru/problem.php?contest=0&problem=294