| 题目名称 | 3782. [CSP 2022S]策略游戏 |
|---|---|
| 输入输出 | game.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:18, 提交:113, 通过率:15.93% | ||||
|
|
100 | 1.469 s | 10.18 MiB | C++ |
|
|
100 | 1.521 s | 10.19 MiB | C++ |
|
|
100 | 1.697 s | 57.84 MiB | C++ |
|
|
100 | 1.828 s | 15.16 MiB | C++ |
|
|
100 | 1.913 s | 16.10 MiB | C++ |
|
|
100 | 2.327 s | 41.61 MiB | C++ |
|
|
100 | 2.483 s | 54.86 MiB | C++ |
|
|
100 | 2.697 s | 51.73 MiB | C++ |
|
|
100 | 2.716 s | 51.73 MiB | C++ |
|
|
100 | 2.746 s | 51.73 MiB | C++ |
| 本题关联比赛 | |||
| CSP2022提高组 | |||
| 20250527CSP-S模拟 | |||
| 20251019新安模拟赛1 | |||
| 关于 策略游戏 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
非常好的线段树:)
| ||||
|
le
2023-09-21 19:11
4楼
| ||||
|
要求区间大于0的最小值
只能想到用平衡树求0的后继了
2023-04-13 22:03
3楼
| ||||
|
N年OI一场空,开了 long long 不改 INF 还是一场空
2022-10-30 12:59
2楼
| ||||
|
洛谷AC,本机TLE
这就是分块的魅力 | ||||
【题目描述】
小 L 和小 Q 在玩一个策略游戏。
有一个长度为 $n$ 的数组 $A$ 和一个长度为 $m$ 的数组 $B$,在此基础上定义一个大小为 $n \times m$ 的矩阵 $C$,满足 $C_{i j} = A_i \times B_j$。所有下标均从 $1$ 开始。
游戏一共会进行 $q$ 轮,在每一轮游戏中,会事先给出 $4$ 个参数 $l_1, r_1, l_2, r_2$,满足 $1 \le l_1 \le r_1 \le n$、$1 \le l_2 \le r_2 \le m$。
游戏中,小 L 先选择一个 $l_1 \sim r_1$ 之间的下标 $x$,然后小 Q 选择一个 $l_2 \sim r_2$ 之间的下标 $y$。定义这一轮游戏中二人的得分是 $C_{x y}$。
小 L 的目标是使得这个得分尽可能大,小 Q 的目标是使得这个得分尽可能小。同时两人都是足够聪明的玩家,每次都会采用最优的策略。
请问:按照二人的最优策略,每轮游戏的得分分别是多少?
【输入格式】
第一行输入三个正整数 $n, m, q$,分别表示数组 $A$,数组 $B$ 的长度和游戏轮数。
第二行:$n$ 个整数,表示 $A_i$,分别表示数组 $A$ 的元素。
第三行:$m$ 个整数,表示 $B_i$,分别表示数组 $B$ 的元素。
接下来 $q$ 行,每行四个正整数,表示这一次游戏的 $l_1, r_1, l_2, r_2$。
【输出格式】
输出共$q$行,每行一个整数,分别表示每一轮游戏中,小 L 和小 Q 在最优策略下的得分。
【样例1输入】
3 2 2 0 1 -2 -3 4 1 3 1 2 2 3 2 2
【样例1输出】
0 4
【样例1解释】
这组数据中,矩阵 $C$ 如下:
$$ \begin{bmatrix} 0 & 0 \\ -3 & 4 \\ 6 & -8 \end{bmatrix} $$
在第一轮游戏中,无论小 L 选取的是 $x = 2$ 还是 $x = 3$,小 Q 都有办法选择某个 $y$ 使得最终的得分为负数。因此小 L 选择 $x = 1$ 是最优的,因为这样得分一定为 $0$。
而在第二轮游戏中,由于小 L 可以选 $x = 2$,小 Q 只能选 $y = 2$,如此得分为 $4$。
【样例2输入】
6 4 5 3 -1 -2 1 2 0 1 2 -1 -3 1 6 1 4 1 5 1 4 1 4 1 2 2 6 3 4 2 5 2 3
【样例2输出】
0 -2 3 2 -1
【样例下载】
【数据规模与约定】
对于所有数据,$1 \le n, m, q \le {10}^5$,$-{10}^9 \le A_i, B_i \le {10}^9$。对于每轮游戏而言,$1 \le l_1 \le r_1 \le n$,$1 \le l_2 \le r_2 \le m$。
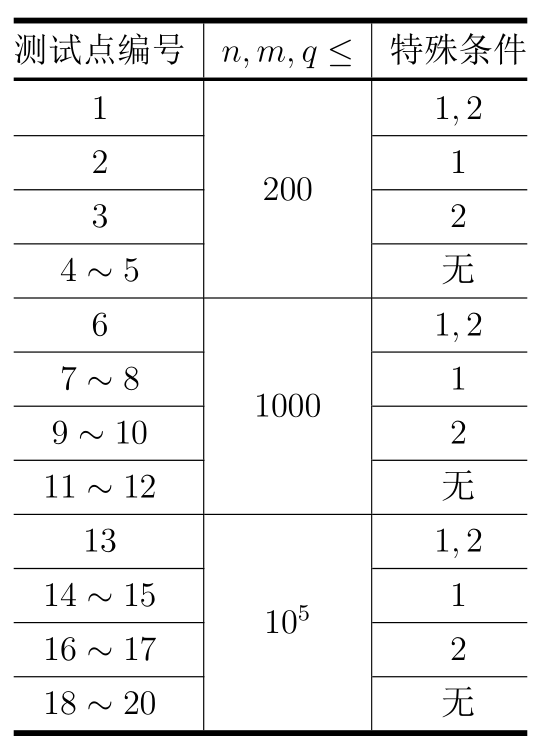
其中,特殊性质 1 为:保证 $A_i, B_i > 0$。
特殊性质 2 为:保证对于每轮游戏而言,要么 $l_1 = r_1$,要么 $l_2 = r_2$。
【来源】
CSP 2022提高组 Task2