| 题目名称 | 1727. [BOI2002]双调路径 |
|---|---|
| 输入输出 | bic.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 100 ms (0.1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 12 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:5, 提交:35, 通过率:14.29% | ||||
|
|
100 | 0.016 s | 154.02 MiB | C++ |
|
|
100 | 0.066 s | 9.65 MiB | C++ |
|
|
100 | 0.084 s | 9.60 MiB | C++ |
|
|
100 | 0.129 s | 23.12 MiB | C++ |
|
|
100 | 0.426 s | 397.50 MiB | C++ |
|
|
83 | 0.056 s | 5.56 MiB | C++ |
|
|
83 | 0.526 s | 13.23 MiB | C++ |
|
|
75 | 0.053 s | 5.56 MiB | C++ |
|
|
66 | 0.590 s | 23.61 MiB | C++ |
|
|
66 | 1.621 s | 5.24 MiB | C++ |
| 关于 双调路径 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
2015-03-26 17:55
3楼
| ||||
|
给耗时为0的路径跪了
2015-03-25 19:26
2楼
| ||||
|
费用和耗时都相同的路线算作同一条
刚看到这题的时候吓我一跳……然后发现这句话,然后就水了
2014-10-09 20:19
1楼
| ||||
【题目描述】
Byteland的收费高速公路网正迅速成长。它已变得如此稠密,以至于最佳路线的选择成为了一个严重的问题。高速公路网由连接城市的双向道路组成。每一条这样的道路都有耗时和通行费两个参数。
一条路线由旅途中连续经过的道路组成。路线的总耗时是途中经过所有道路耗时的总和。而路线的总费用就是所有道路的通行费之和。耗时越少,花费越小,路线就越优。严格地,一条路线比另一条路线更优,当且仅当它比后者更快,而且费用不超过后者,或者它的费用比后者更低,且耗时不超过后者。我们称一条连接两个城市的路线是最优的,当且仅当没有一条连接这两个城市的路线比它更优。不幸的是,并不一定总是存在最优路线——可能有若干条无法比较的路线,或者根本没有路线。
下图展示了高速公路网的一个例子。每条道路旁都写着一对数字:通行费和耗时。
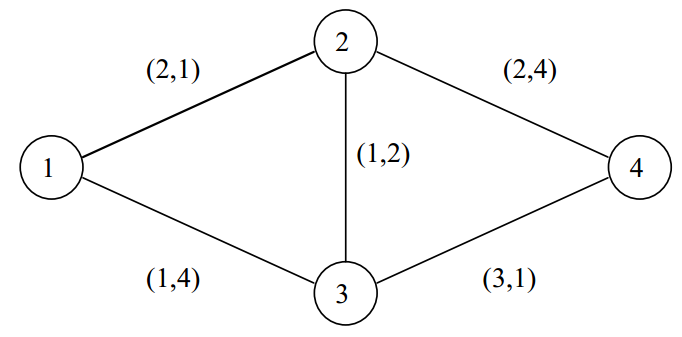
让我们考虑从城市1到城市4的四条不同路线,以及它们的通行费和耗时:1-2-4(费用4,耗时5),1-3-4(费用4,耗时5),1-2-3-4(费用6,耗时4),1-3-2-4(费用4,耗时10)。
路线1-3-4和1-2-4比1-3-2-4更优。有两种方案,分别让费用和时间最小:第一种是费用4,耗时5(路线1-2-4和1-3-4),第二种是费用6,耗时4(路线1-2-3-4)。当选择路线时,我们需要决定走得快但花更多钱(路线1-2-3-4),或者走得慢但便宜(1-3-4或1-2-4)。
写一个程序:
·读入高速公路网,路线的起点和终点。
·计算从起点到终点的不同最优路线数量,但费用和耗时都相同的路线算作同一条,我们只对最小的费用-时间数字对感兴趣。
·输出结果
【输入格式】
第一行有四个整数:城市数n(1<=n<=100),道路数m(0<=m<=300),起点s和终点e,1<=s,e<=n,s≠e。接下来m行描述了道路,每条道路一行。每行有四个空格隔开的整数:道路的两个端点p和r,1<=p,r<=n,p≠r,费用c,0<=c<=100,耗时t,0<=t<=100。两座城市间可能有不止一条道路。
【输出格式】
你的程序应该输出一行一个整数,即从s到e,不同的最优费用-耗时数字对的数量。
【样例输入】
4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4
【样例输出】
2
【提示】
样例即为题目中的例子
【来源】
BOI 2002 Bicriterial routing