| 题目名称 | 3661. [统一省选 2022]填树 |
|---|---|
| 输入输出 | tree.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 本题关联比赛 | |||
| 20250527树形DP练习 | |||
| 省选2022Day1复现 | |||
| 关于 填树 的近10条评论(全部评论) |
|---|
- 将当前节点 $i$ 的权值修改为一个正整数 $x$,需满足 $l_i\leq x\leq r_i$。其中 $l_i,r_i$ 是输入中给出的两个正整数。
- 结束修改过程,或移动到一个与当前节点相邻的权值为 0 的节点(如果不存在这样的节点,则必须结束修改过程)。
- 在修改结束后,可以得到多少棵不同的树,满足树上非零权值的最大值和最小值的差小于等于 $K$?其中 $K$ 是输入中给出的一个正整数。
- 这些满足条件的树的权值之和为多少?(树的权值定义为这棵树上所有节点的权值之和)
- KK 至少会修改一个节点(初始节点)。
- 实质上 KK 会修改树上的任意一条路径,最后需要满足这条路径上的点的权值最大值和最小值之差小于等于 $K$。
【题目描述】
有一棵 $n$ 个节点的无根树,刚开始树上每个节点的权值均为 0。KK 想对这棵树进行一些修改,他会任选一个节点作为初始的当前节点,然后重复以下动作:
现在 KK 有两个问题:
你需要输出这两个问题的答案模 $10^9+7$。我们认为两棵树不同当且仅当至少存在一个节点的权值不同。
温馨提示:
【输入格式】
第一行两个正整数 $n, K$,表示节点数和权值差的最大值。
接下来 $n$ 行,每行两个正整数 $l_i,r_i$,表示第 $i$ 个节点修改后权值的最小值和最大值。
接下来 $n-1$ 行,每行两个正整数 $u_i,v_i$,表示节点 $u_i$ 和 $v_i$ 之间有一条边。数据保证形成一棵树。
【输出格式】
输出两行,每行一个整数,分别表示第一问和第二问的答案模 $10^9+7$ 的值。注意,如果你不打算回答第二问,请在第二行任意输出一个整数。如果输出文件只有一行,则会因格式不符合要求被判 0 分。
【样例输入】
3 1 2 3 3 5 4 6 1 2 1 3
【样例输出】
14 78
【样例说明】
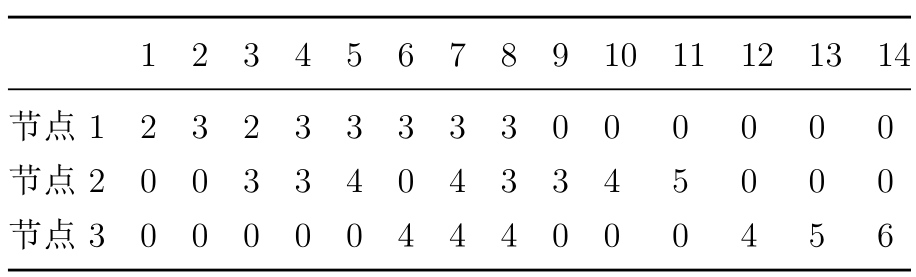
表格中列出了全部 14 棵满足条件的树,将这些树的权值加起来为 78。
【数据规模与约定】
对于100%的数据,$1\leq n\leq 200,1\leq l_i\leq r_i\leq 10^9,1\leq K\leq 10^9$。
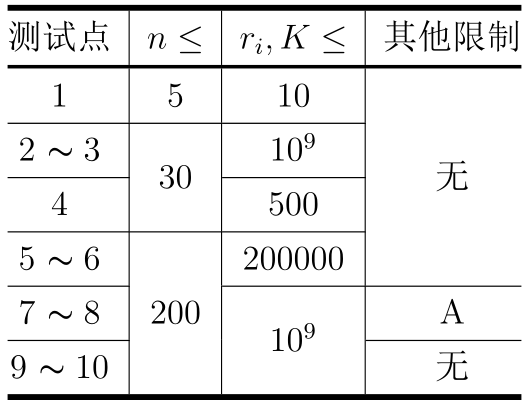
特殊限制 A:所有点构成一条链, 编号为 $i$ 的点和编号为 $i+1$ 的点之间有连边
【评分标准】
本题共 10 个测试点,每个测试点 10 分。其中回答正确第一问可得 7 分,回答正确第二问可得 3 分。
【来源】
2022 统一省选 Day1 Task2