| 题目名称 | 2640. [HZOI 2015] 帕秋莉的超级多项式V2 |
|---|---|
| 输入输出 | PatchouliGo.in/out |
| 难度等级 | ★★ |
| 时间限制 | 250 ms (0.25 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:7, 提交:14, 通过率:50% | ||||
|
|
100 | 1.600 s | 20.29 MiB | C++ |
|
|
100 | 1.739 s | 2.29 MiB | C++ |
|
|
100 | 2.399 s | 0.29 MiB | C++ |
|
|
100 | 3.279 s | 0.54 MiB | C++ |
|
|
100 | 3.386 s | 20.06 MiB | C++ |
|
|
100 | 3.389 s | 0.29 MiB | C++ |
|
|
100 | 9.346 s | 0.17 MiB | Pascal |
|
|
0 | 1.456 s | 0.29 MiB | C++ |
|
|
0 | 1.709 s | 20.29 MiB | C++ |
|
|
0 | 1.759 s | 20.29 MiB | C++ |
| 关于 帕秋莉的超级多项式V2 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
Orz驴蛋蛋!
2017-03-30 14:21
4楼
| ||||
|
这题一定是卡快读的【雾
2017-03-29 20:01
3楼
| ||||
|
数据有误请找驴蛋蛋...
我好菜啊...我宛若一盘驴蛋蛋....
2017-03-29 19:02
2楼
| ||||
|
orz驴蛋蛋
2017-03-29 17:26
1楼
| ||||
2640. [HZOI 2015] 帕秋莉的超级多项式V2
★★ 输入文件:PatchouliGo.in
输出文件:PatchouliGo.out
简单对比时间限制:0.25 s 内存限制:256 MiB
在幻想乡,帕秋莉·诺蕾姬(パチュリー·ノーレッジ)是以宅在图书馆闻名的魔法使。
其语文,数学,英语,物理,化学,生物,政治,历史,地理,哲♂学,无所不通晓。

这天魔理沙又来图书馆<del>偷</del>窃算法导论,不由又被咲夜抓到了。
这次帕Q要亲自用算多项式的方式惩罚摸你傻,如果摸你傻算出来了就放她走。
问题就是求关于自变量z的函数$F(z)=$ 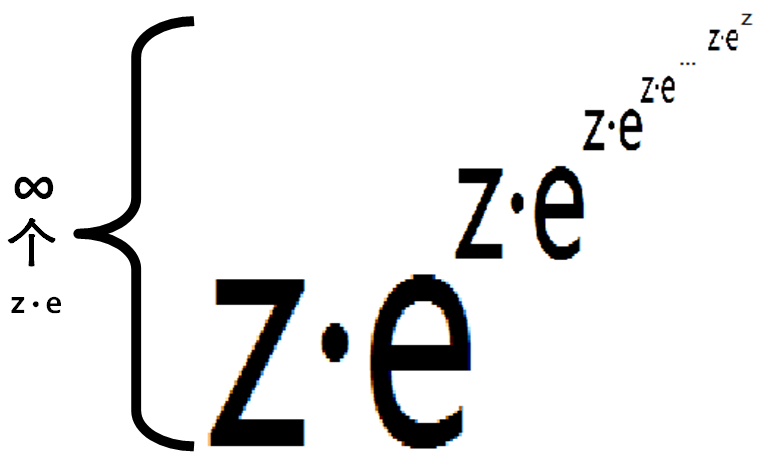
泰勒展开后的 $[z^n] $项系数乘上$n!$之后 $\mod p$ 的值(其中·表示乘法运算,e为自然对数)
你可能会用到的知识:
泰勒展开的作用是将一个式子展开成与其等价的无限项多项式的形式
泰勒展开意义下 $ e^z=\frac{z^0}{0!}+\frac{z^1}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\dots\ $
若多项式 $F(z)$ 满足$ F(z)=a_0+a_1 z^1+a_2 z^2+a_3 z^3...$ 那么$ [z^n]F(z)=a_n $
【输入格式】
第一行一个整数$T$
接下来$T$行每行两个整数$n,p$
【输出格式】
每行一个整数表示所需的值
【样例输入】
1
3 3
【样例输出】
0
【解释】
答案本应该是3,在mod 3意义下为0
【提示】
由于出题人心情不好所以不存在梯度数据
$1 \le T,n,p\le 5·10^4$
【来源】
某次出题和唐教主撞车的驴蛋蛋...