| 题目名称 | 1756. [NOI 2008] 糖果雨 |
|---|---|
| 输入输出 | noi2008_candy.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:15, 提交:41, 通过率:36.59% | ||||
|
|
100 | 1.277 s | 99.65 MiB | C++ |
|
|
100 | 1.298 s | 73.40 MiB | C++ |
|
|
100 | 1.307 s | 50.12 MiB | C++ |
|
|
100 | 1.309 s | 69.26 MiB | C++ |
|
|
100 | 1.324 s | 99.65 MiB | C++ |
|
|
100 | 1.946 s | 124.73 MiB | C++ |
|
|
100 | 2.023 s | 124.73 MiB | C++ |
|
|
100 | 2.266 s | 70.18 MiB | C++ |
|
|
100 | 2.290 s | 69.41 MiB | C++ |
|
|
100 | 2.320 s | 124.73 MiB | C++ |
| 本题关联比赛 | |||
| 4043级2023省选模拟赛2 | |||
| 关于 糖果雨 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
124.73MB……论卡内存的重要性……
| ||||
【题目描述】
有一个美丽的童话:在天空的尽头有一个”糖果国”,这里大到摩天大厦,小到小花小草都是用糖果建造而成的。
更加神奇的是,天空中飘满了五颜六色的糖果云,很快糖果雨密密麻麻从天而落,红色的是草莓糖,黄色的是柠檬糖,绿色的是薄荷糖,黑色的是巧克力糖……
这时糖果国的小朋友们便会拿出大大小小的口袋来接天空中落下的糖果,拿回去与朋友们一起分享。
对糖果情有独钟的小 $Z$ 憧憬着能够来到这样一个童话的国度。
所谓日有所思,夜有所梦,这天晚上小 $Z$ 梦见自己来到了”糖果国”。
他惊喜地发现,任何时候天空中所有的云朵颜色都不相同,不同颜色的云朵在不断地落下相应颜色的糖果。
更加有趣的是所有的云朵都在做着匀速往返运动,不妨想象天空是有边界的,而所有的云朵恰好在两个边界之间做着往返运动。
每一个单位时间云朵向左或向右运动一个单位,当云朵的左界碰到天空的左界,它会改变方向向右运动;
当云朵完全移出了天空的右界,它会改变方向向左运动。
我们不妨把天空想象为一个平面直角坐标系,而云朵则抽象为线段(线段可能退化为点):
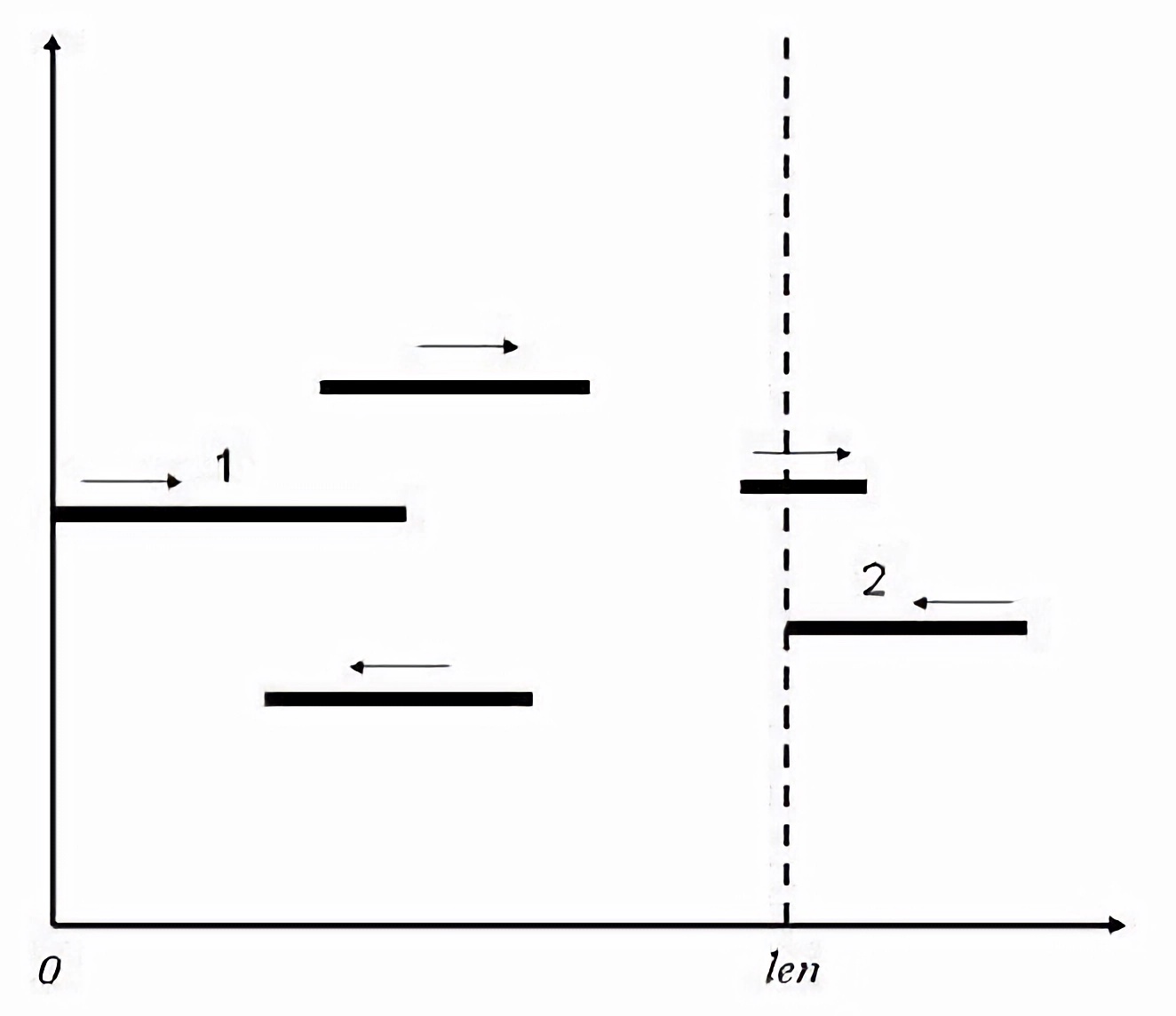
如上图,不妨设天空的左界为 $0$,右界为 $len$。
图中共有 $5$ 片云朵,其中标号为 $1$ 的云朵恰好改变方向向右运动,标号为 $2$ 的云朵恰好改变方向向左运动。
忽略云朵的纵坐标,它们在运动过程中不会相互影响。
小 $Z$ 发现天空中会不断出现一些云朵(某个时刻从某个初始位置开始朝某个方向运动),而有的云朵运动到一定时刻就会从天空中消失,而在运动的过程中糖果在不断地下落。
小 $Z$ 决定拿很多口袋来接糖果,口袋容量是无限的,但袋口大小却是有限的。
例如在时刻 $T$ 小 $Z$ 拿一个横坐标范围为 $[L,R]$ 的口袋来接糖果,如果 $[L,R]$ 存在一个位置 $x$,该位置有某种颜色的糖果落下,则认为该口袋可接到此种颜色的糖果。
极端情况下,袋口区间可能是一个点,譬如 $[0,0]$、$[1,1]$,但仍然可以接到相应位置的糖果。
通常可以接到的糖果总数会很大,因而小 $Z$ 想知道每一次(即拿出口袋的一瞬间)他的口袋可以接到多少种不同颜色的糖果。
糖果下落的时间忽略不计。
【输入格式】
第一行有两个正整数 $n,len$,分别表示事件总数以及天空的“边界”。
接下来 $n$ 行每行描述一个事件,所有的事件按照输入顺序依次发生。
每行的第一个数 $k(k=1,2,3)$ 分别表示事件的类型,分别对应三种事件:插入事件,询问事件以及删除事件。
输入格式如下:
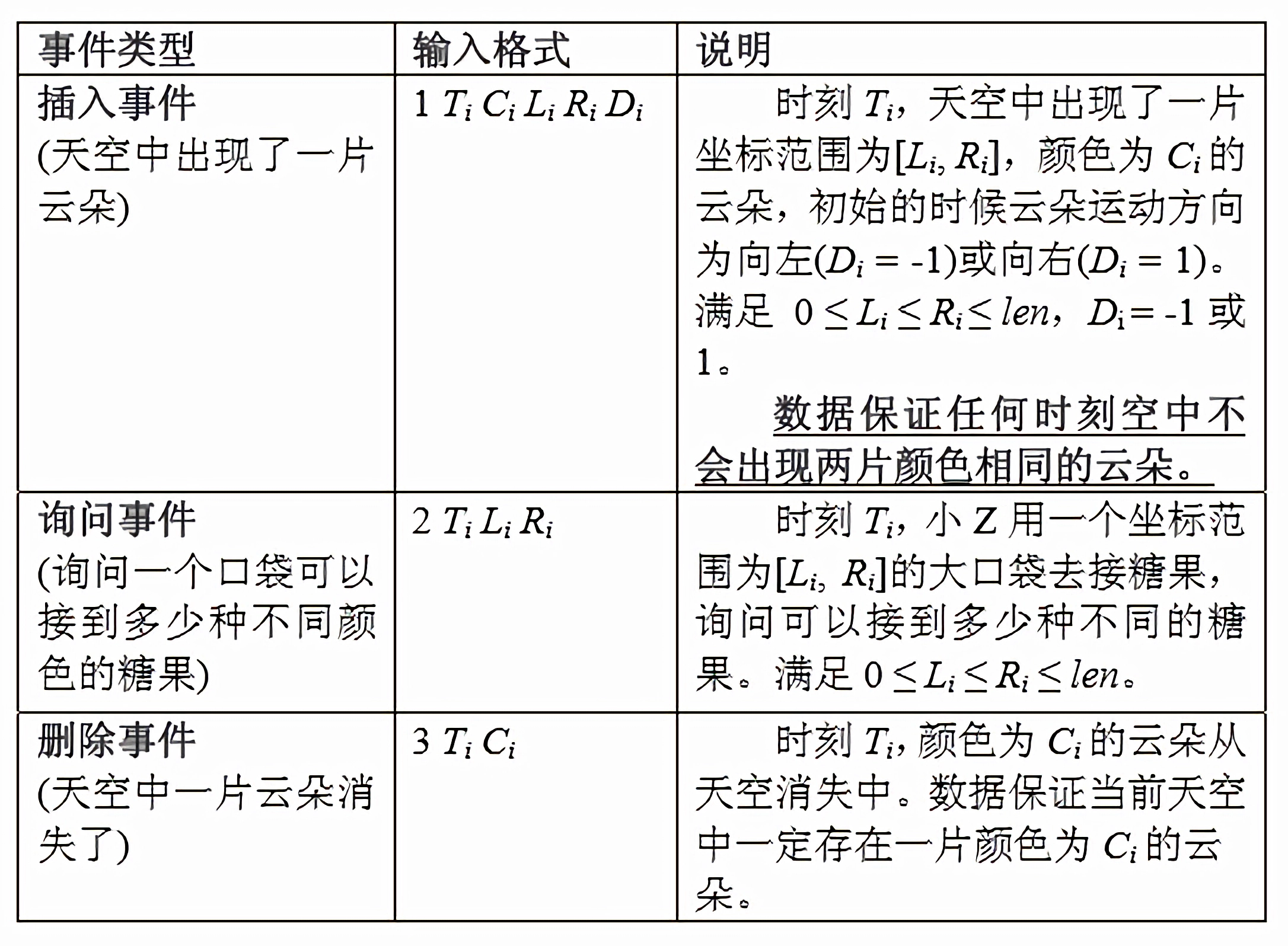
【输出格式】
对于每一个询问事件,输出中应包含相应的一行,为该次询问的答案,即口袋可以接到多少种不同的糖果。
【样例1输入】
10 10 1 0 10 1 3 -1 2 1 0 0 2 11 0 10 2 11 0 9 1 11 13 4 7 1 2 13 9 9 2 13 10 10 3 100 13 3 1999999999 10 1 2000000000 10 0 1 1
【样例1输出】
1 1 0 2 1
【样例1说明】
共 $10$ 个事件,包括 $3$ 个插入事件,$5$ 个询问事件以及 $2$ 个删除事件。
时刻 $0$,天空中出现一片颜色为 $10$ 的云朵,初始位置为 $[1, 3]$ ,方向向左。
时刻 $1$,范围为 $[0, 0]$ 的口袋可以接到颜色为 $10$ 的糖果(云朵位置为 $[0, 2]$ )。
时刻 $11$,范围为 $[0,10]$ 的口袋可以接到颜色为 $10$ 的糖果(云朵位置为 $[10,12]$ )。
时刻 $11$,范围为 $[0, 9]$ 的口袋不能接到颜色为 $10$ 的糖果(云朵位置为 $[10,12]$ )。
时刻 $11$, 天空中出现一片颜色为 $13$ 的云朵, 初始位置为 $[4, 7]$ , 方向向右。
时刻 $13$,范围为 $[9, 9]$ 的口袋可以接到颜色为 $10$ (云朵的位置为 $[8,10]$ )和颜色为 $13$ (云朵的位置为 $[6, 9]$ )两种不同的糖果。
时刻 $13$,范围为 $[10 ,10]$ 的口袋仅仅可以接到颜色为 $10$ 的一种糖果(云朵的位置为 $[8,10]$ ),而不可以接到颜色为 $13$ 的糖果(云朵的位置为 $[6, 9]$ ),。
时刻 $100$, 颜色为 $13$ 的云朵从天空中消失。
时刻 $1999999999$,颜色为 $10$ 的云朵从天空中消失。
时刻 $2000000000$,天空中又出现一片颜色为 $10$ 的云朵,初始位置为 $[0, 1]$ ,方向向右。
【数据规模与约定】
对于所有的数据,$0≤T_i≤2,000,000,000,1≤C_i≤1,000,000$。
数据保证 ${Ti}$ 为非递减序列即 $T_1≤T_2≤…≤T_{n−1}≤T_n$。
对于所有的插入事件,令 $P_i=R_i–L_i$,即 $P_i$ 表示每片云朵的长度。 