| 题目名称 | 2300. [APIO 2016] 烟花表演 |
|---|---|
| 输入输出 | fireworks.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 80 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:10, 提交:20, 通过率:50% | ||||
|
|
100 | 3.414 s | 23.20 MiB | C++ |
|
|
100 | 4.616 s | 36.93 MiB | C++ |
|
|
100 | 4.812 s | 7.18 MiB | C++ |
|
|
100 | 5.184 s | 8.11 MiB | C++ |
|
|
100 | 5.332 s | 10.34 MiB | C++ |
|
|
100 | 5.622 s | 7.17 MiB | C++ |
|
|
100 | 6.183 s | 7.17 MiB | C++ |
|
|
100 | 7.419 s | 19.86 MiB | C++ |
|
|
100 | 9.428 s | 78.28 MiB | C++ |
|
|
100 | 10.184 s | 33.50 MiB | C++ |
| 关于 烟花表演 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
pbds大法好
| ||||
|
| ||||
LL k=(LL)c[1].size()-points.size()没加(LL)…… DFS爆栈…… 退役选手身败名裂…… | ||||
|
韩国人居然用auto来指定类型。。。CE得好惨。。。还好有两份是能编译的
(2s的时限是不是太长了? | ||||
【问题描述】
烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全,烟花被安置在远离开关的位置上,通过一些导火索与开关相连。导火索的连接方式形成一棵树,烟花是树叶,如[图1]所示。火花从开关出发,沿导火索移动。每当火花抵达一个分叉点时,它会扩散到与之相连的所有导火索,继续燃烧。导火索燃烧的速度是一个固定常数。[图1]展示了六枚烟花{$E_1,E_2,\dots,E_6$}的连线布局,以及每根导火索的长度。图中还标注了当在时刻$0$从开关点燃火花时,每一发烟花的爆炸时间。
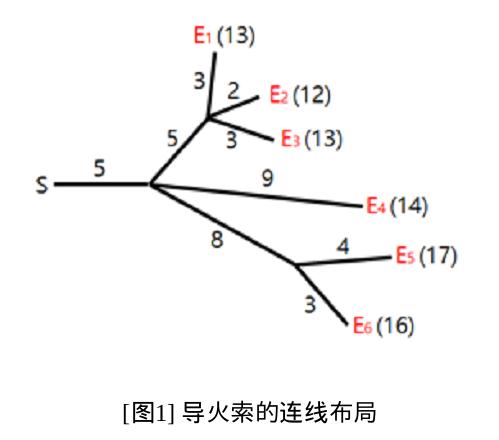
Hyunmin为烟花表演设计了导火索的连线布局。不幸的是,在他设计的布局中,烟花不一定同时爆炸。我们希望修改一些导火索的长度,让所有烟花在同一时刻爆炸。例如,为了让[图1]中的所有烟花在时刻$13$爆炸,我们可以像[图2]中左边那样调整导火索长度。类似地,为了让[图1]中的所有烟花在时刻$14$爆炸,我们可以像[图2]中右边那样调整长度。
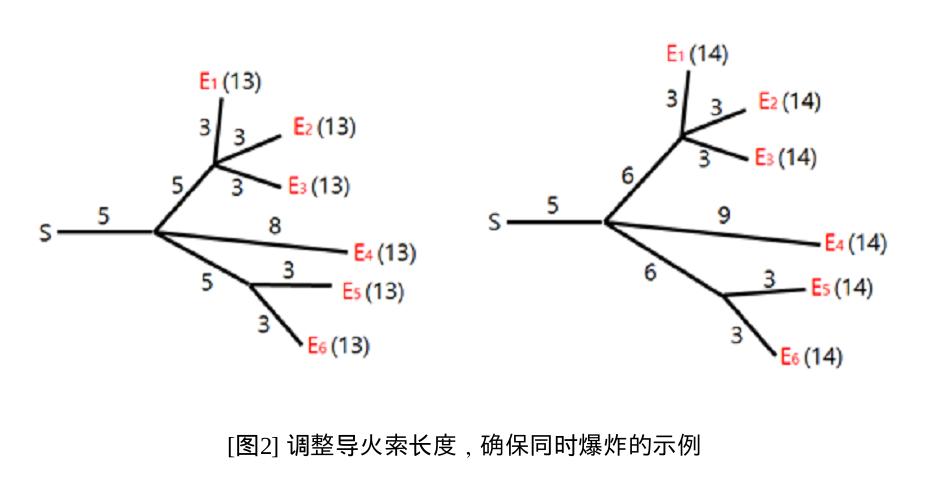
修改导火索长度的代价等于修改前后长度之差的绝对值。例如,将[图1]中布局修改为[图2]左边布局的总代价为$6$,而将[图1]中布局修改为[图2]右边布局的总代价为$5$.
导火索的长度可以被减为$0$,同时保持连通性不变。
给定一个导火索的连线布局,你需要编写一个程序,去调整导火索长度,让所有的烟花在同一时刻爆炸,并使得代价最小。
【输入格式】
所有的输入均为正整数。令$N$代表分叉点的数量,$M$代表烟花的数量。分叉点从$1$到$N$编号,编号为$1$的分叉点是开关。烟花从$N+1$到$N+M$编号。
输入格式如下:
$N\ M$
$P_2\ C_2$
$P_3\ C_3$
$\dots$
$P_N\ C_N$
$P_{N+1}\ C_{N+1}$
$\dots$
$P_{N+M}\ C_{N+M}$
其中$P_i$满足$1 \leq P_i < i$,代表和分叉点或烟花$i$相连的分叉点。$C_i$代表连接它们的导火索长度($1 \leq C_i \leq 10^9$)。除开关外,每个分叉点和多于$1$条导火索相连,而每发烟花恰好与$1$条导火索相连。
【输出格式】
输出调整导火索长度,让所有烟花同时爆炸,所需要的最小代价。
【样例输入】
4 6 1 5 2 5 2 8 3 3 3 2 3 3 2 9 4 4 4 3
【样例输出】
5
【分数】
子任务1(7分,在COGS上为10个测试点):$N = 1,1 \leq M \leq 100$。
子任务2(19分,在COGS上为20个测试点):$1 \leq N + M \leq 300$且开关到任意烟花的距离不超过$300$。
子任务3(29分,在COGS上为25个测试点):$1 \leq N + M \leq 5,000$。
子任务4(45分,在COGS上为25个测试点):$1 \leq N + M \leq 300,000$。
【来源】
APIO2016 第二题
因为评测系统不资瓷捆绑测试,所以分数的划分和原题不同