| 题目名称 | 2568. K边最短路 |
|---|---|
| 输入输出 | kminpath.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:4, 提交:5, 通过率:80% | ||||
|
|
100 | 0.056 s | 4.15 MiB | C++ |
|
|
100 | 0.066 s | 2.18 MiB | C++ |
|
|
100 | 0.071 s | 3.99 MiB | C++ |
|
|
100 | 0.079 s | 4.81 MiB | C++ |
|
|
0 | 0.037 s | 3.68 MiB | C++ |
| 关于 K边最短路 的近10条评论(全部评论) |
|---|
【题目描述】
已知有向图 $G$,请编程计算从点 $i$ 到点 $j$ 经过 $k$ 条边的最短路。
【输入格式】
第一行三个正整数 $N$、$M$ 和 $K$,分别表示有向图顶点数、边数和题意中的 $K$ 值。
接下来 $M$ 行,每行 $3$ 个正整数 $x$、$y$ 和 $z$,表示 $x$ 到 $y$ 有一条权值为 $z$ 有向边。
【输出格式】
输出 $N$ 行 $N$ 列矩阵;
第 $i$ 行,第 $j$ 列的整数表示点 $i$ 到点 $j$ 经过 $k$ 条边的最短路;
如果点 $i$ 到点 $j$ 经过 $k$ 条边的路径不存在,则输出 $0$;
【样例输入1】
4 5 2 1 2 5 1 3 10 2 3 6 2 4 9 3 4 3
【样例输出1】
0 0 11 13 0 0 0 9 0 0 0 0 0 0 0 0
【样例1说明】
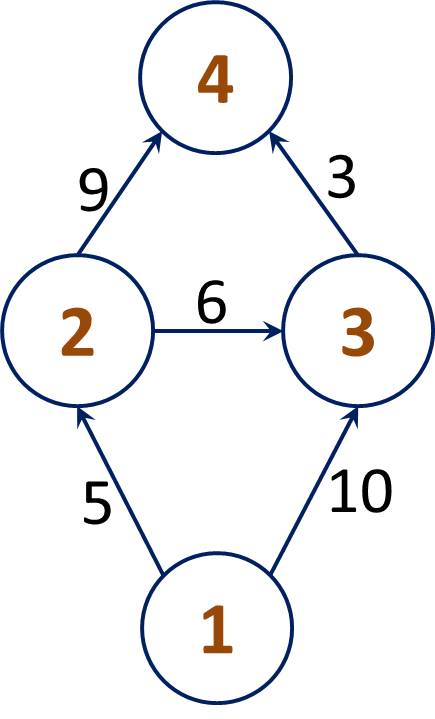
如图所示,任意两点间有 $2$ 条边的路径如下:
$1 \longrightarrow 3:1 \rightarrow 2 \rightarrow 3;1 条路,最短 11$
$1 \longrightarrow 4:1 \rightarrow 2 \rightarrow 4,1 \rightarrow 3 \rightarrow 4;2 条路,最短 13$
$2 \longrightarrow 4:2 \rightarrow 3 \rightarrow 4;1 条路,最短 9$
【样例输入2】
5 8 3 1 2 1 1 3 2 1 4 3 2 3 2 2 5 3 3 4 1 3 5 3 4 5 2
【样例输出2】
0 0 0 4 5 0 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
【样例2说明】
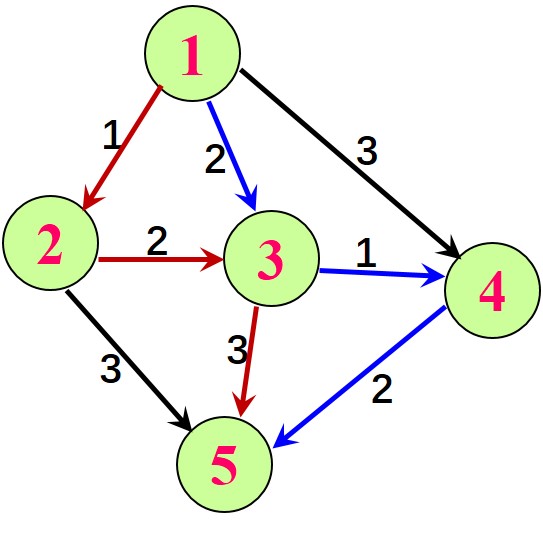
如图所示,任意两点间有 $3$ 条边的路径如下:
$1 \longrightarrow 4:1 \rightarrow 2 \rightarrow 3 \rightarrow 4;1 条路,最短 4$
$1 \longrightarrow 5:1 \rightarrow 2 \rightarrow 3 \rightarrow 5,1 \rightarrow 3 \rightarrow 4 \rightarrow 5;2 条路,最短 5$
$2 \longrightarrow 5:2 \rightarrow 3 \rightarrow 4 \rightarrow 5;1 条路,最短 5$
【数据规模】
$100\%$ 的数据,$1 \leq n \leq 100,1 \leq k \leq 15$,所有边权之和不超过 $1000,0000$.
【来源】
$Mr$ $chengyy$