| 题目名称 | 1466. 完全排序网络 |
|---|---|
| 输入输出 | sortingnet.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:17, 提交:39, 通过率:43.59% | ||||
|
|
100 | 0.077 s | 0.32 MiB | C++ |
|
|
100 | 0.078 s | 1.84 MiB | C++ |
|
|
100 | 0.079 s | 1.84 MiB | C++ |
|
|
100 | 0.081 s | 1.84 MiB | C++ |
|
|
100 | 0.085 s | 0.20 MiB | Pascal |
|
|
100 | 0.105 s | 0.32 MiB | C++ |
|
|
100 | 0.113 s | 1.82 MiB | C++ |
|
|
100 | 0.115 s | 0.17 MiB | Pascal |
|
|
100 | 0.118 s | 0.17 MiB | Pascal |
|
|
100 | 0.120 s | 1.84 MiB | C++ |
| 本题关联比赛 | |||
| 2022级数学专题练习赛4 | |||
| 关于 完全排序网络 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
判断完全排序网络是NPC的,这个正解算法是错的,维护不等式会丢失信息,但是反例应该不多。。。
2017-07-05 19:50
8楼
| ||||
|
For(j,1,n) num[i]=rand()%10086;
喵了个咪的,居然过了7组QAQ  我知道原题是想我TopSort | ||||
|
回复 @Chenyao : 神奇
2013-12-30 20:03
6楼
| ||||
|
回复 @Chenyao :
这只是个装逼名词而已……定义了个inequ[i][j]表示当前已知i>=j | ||||
|
回复 @cstdio :
弱弱问下,什么是不等式的信息
2013-12-27 13:32
4楼
| ||||
|
回复 @Chenyao :
已修复(喵的人家原题明明是让即时修改不等式信息好嘛只是我的数据淼而已(╯‵□′)╯︵┻━┻) | ||||
|
随机多组数据,然后根据排序,判断是否都正确 @cstdio 最后一个点数据20w,题目最大数据10w。。直接爆数组了。。。。
| ||||
|
好神奇
现在不看题解已经做不出来了
2013-12-25 18:37
1楼
| ||||
【题目描述】
排序网络是这样一个模型:
有 $n$ 条水平的导线,由上至下分别标号为 $1$ 至 $n$,导线与导线之间不相交。在任意两导线之间可以搭上“电桥”。每条导线的左端放置一数字,数字沿导线由左向右同步运行,当遇上一电桥时,比较电桥两端的两根导线上的数字,将其中较大的放到上面的导线上,而将较小的放到下面的导线上,然后继续运行,保证同一时刻最多只有一个电桥。(如图)
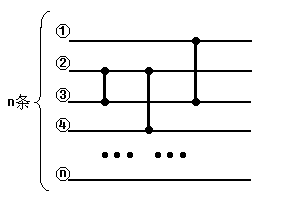
若一个 $n$ 行的排序网络共包含 $m$ 个电桥,对于左端输入的任意顺序的数列,都能在右端得到一个由大到小的数列,我们称这个排序网络是一个完全排序网络。
我们的程序需要做的,就是判断一个排序网络是否是一个完全排序网络。
【输入格式】
第一行是一个整数 $N$,表示排序网络的行数;
第二行是一个整数 $M$,表示排序网络的电桥数;
接下来的 $M$ 行,每行有两个整数 $i,j$,表示导线 $i$ 和 $j$ 之间有一条电桥。
电桥按从左向右的顺序依次给出。
【输出格式】
一行。若这个排序网络是完全排序网络,那么输出"$Yes!$",否则输出"$No!$"。
当然,你的输出中不包含引号。
【样例1输入】
6 15 1 2 2 3 3 4 4 5 5 6 1 2 2 3 3 4 4 5 1 2 2 3 3 4 1 2 2 3 1 2
【样例1输出】
Yes!
【样例1说明】
样例描述了一个等价于 $N = 6$ 的冒泡排序法的排序网络;
【样例2输入输出】
点击下载样例2
【数据规模】
对于 $40\%$ 的数据,$N \leq 10,M \leq 100$;
对于 $100\%$ 的数据,$N \leq 100,M \leq 200000$。
【来源】
$NOI1999$北京集训队训练题
杨江明,《论数学策略在信息学问题中的应用》,$IOI2000$国家集训队论文集