| 题目名称 | 4090. [NOIP 2024]遗失的赋值 |
|---|---|
| 输入输出 | assign.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:4, 通过率:25% | ||||
|
|
100 | 1.236 s | 4.86 MiB | C++ |
|
|
20 | 6.782 s | 310.55 MiB | C++ |
|
|
20 | 7.134 s | 310.54 MiB | C++ |
|
|
0 | 0.059 s | 3.36 MiB | C++ |
| 本题关联比赛 | |||
| 2025.1.14 | |||
| 关于 遗失的赋值 的近10条评论(全部评论) |
|---|
【题目描述】
小 F 有 $n$ 个变量 $x_1, x_2, \ldots , x_n$。每个变量可以取 $1$ 至 $v$ 的整数取值。
小 F 在这 $n$ 个变量之间添加了 $n - 1$ 条二元限制,其中第 $i$($1 \leq i \leq n - 1$)条限制为:若 $x_i = a_i$,则要求 $x_{i+1} = b_i$,且 $a_i$ 与 $b_i$ 为 $1$ 到 $v$ 之间的整数;当 $x_i \neq a_i$ 时,第 $i$ 条限制对 $x_{i+1}$ 的值不做任何约束。除此之外,小 F 还添加了 $m$ 条一元限制,其中第 $j$($1 \leq j \leq m$)条限制为:$x_{c_j} = d_j$。
小 F 记住了所有 $c_j$ 和 $d_j$ 的值,但把所有 $a_i$ 和 $b_i$ 的值都忘了。同时小 F 知道:存在给每一个变量赋值的方案同时满足所有这些限制。
现在小 F 想知道,有多少种 $a_i, b_i$($1 \leq i \leq n - 1$)取值的组合,使得能够确保至少存在一种给每个变量 $x_i$ 赋值的方案可以同时满足所有限制。由于方案数可能很大,小 F 只需要你输出方案数对 $10^9 + 7$ 取模的结果。
【输入格式】
本题包含多组测试数据。
输入的第一行包含一个整数 $T$,表示测试数据的组数。
接下来包含 $T$ 组数据,每组数据的格式如下:
第一行包含三个整数 $n, m, v$,分别表示变量个数、一元限制个数和变量的取值上限。
接下来 $m$ 行,第 $j$ 行包含两个整数 $c_j, d_j$,描述一个一元限制。
【输出格式】
对于每组测试数据输出一行,包含一个整数,表示方案数对 $10^9 + 7$ 取模的结果。
【样例1输入】
3 2 1 2 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 2
【样例1输出】
4 3 0
【样例1说明】
对于第一组测试数据,所有可能的 $(a_1, b_1)$ 取值的组合 $(1, 1), (1, 2), (2, 1), (2, 2)$ 都满足限制。例如,$(a_1, b_1) = (1, 1)$ 时,$(x_1, x_2) = (1, 1)$ 满足所有限制,而 $(a_1, b_1) = (2, 2)$ 时,$(x_1, x_2) = (1, 1)$ 与 $(x_1, x_2) = (1, 2)$ 均满足所有限制。
对于第二组测试数据,只有 $(x_1, x_2) = (1, 2)$ 一种可能的变量赋值,因此只有 $(a_1, b_1) = (1, 1)$ 不满足限制,其余三种赋值均满足限制。
对于第三组测试数据,不存在一种变量赋值同时满足 $x_1 = 1$ 和 $x_1 = 2$,因此也不存在满足限制的 $(a_1, b_1)$。
【样例 2】
见选手目录下的 assign/assign2.in 与 assign/assign2.ans。
该样例共有 $10$ 组测试数据,其中第 $i$($1 \leq i \leq 10$)组测试数据满足数据范围中描述的测试点 $i$ 的限制。
【样例 3】
见选手目录下的 assign/assign3.in 与 assign/assign3.ans。
该样例共有 $10$ 组测试数据,其中第 $i$($1 \leq i \leq 10$)组测试数据满足数据范围中描述的测试点 $i + 10$ 的限制。
【数据规模与约定】
对于所有的测试数据,保证:
$1 \leq T \leq 10$,
$1 \leq n \leq 10^9$,$1 \leq m \leq 10^5$,$2 \leq v \leq 10^9$,
对于任意的 $j$($1 \leq j \leq m$),都有 $1 \leq c_j \leq n$,$1 \leq d_j \leq v$。
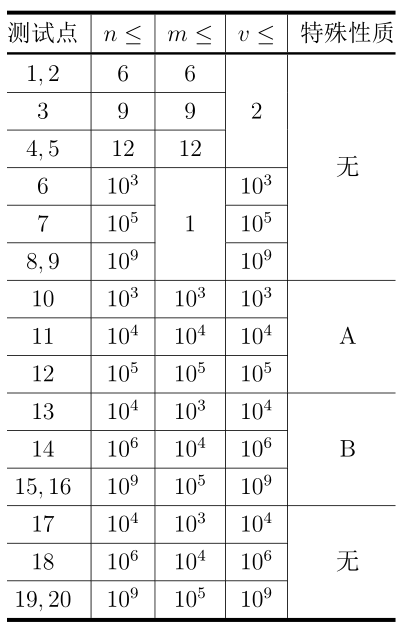
特殊性质 A:保证 $m = n$,且对于任意的 $j$($1 \leq j \leq m$),都有 $c_j = j$。
特殊性质 B:保证 $d_j = 1$。