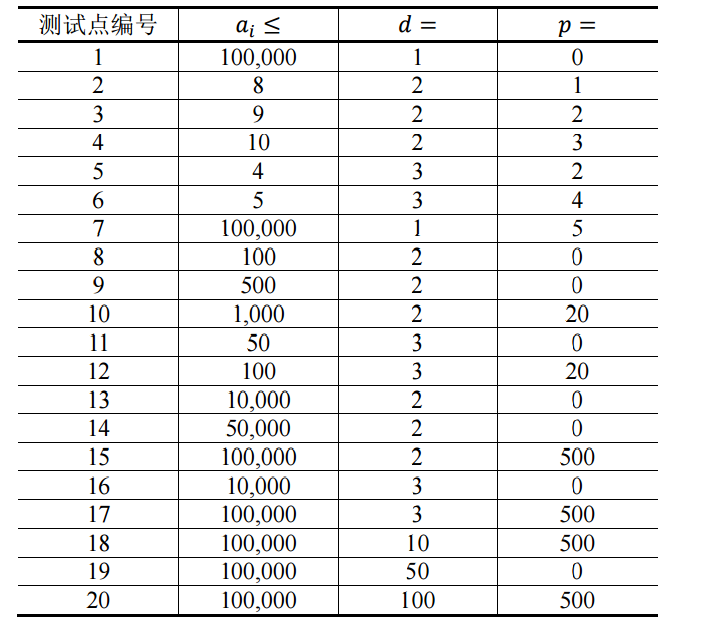
| 题目名称 | 2055. 高维网络 |
|---|---|
| 输入输出 | dimen.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 10.696 s | 71.73 MiB | C++ |
| 关于 高维网络 的近10条评论(全部评论) |
|---|
【题目描述】
现在有一个d维的坐标网格,其中第i维坐标的范围是[0, a[i]]。
在这个范围内建立一个有向图:我们把范围内的每个整点(每一维坐标均为整数的点)当做图上的顶点。
设点A(0, 0, ……, 0), B(a[1], a[2], ……, a[d])。
对于范围内的点(x[1], x[2], ……, x[d]),它会向以下这些点(如果目标点在范围内):
(x[1]+1, x[2], ……, x[d]),
(x[1], x[2]+1, ……, x[d]),
…………
(x[1], x[2], ……, x[d]+1),连有向边。
现在从点A到点B会有若干条路径,路径的条数可以十分简单地算出。
然而不幸的是,范围内有p个点被破坏了(点A和点B不会被破坏),其中第i个点的坐标为(x[i][1], x[i][2], ……, x[i][d])。
你需要算出从点A到点B剩余的路径条数。
由于答案可能很大,你只需要输出它对1000000007 (10^9+7) 取模的结果。
【输入格式】
第一行两个整数d, p
第二行d个整数,第i个数表示a[i]
接下来的p行,每行d个整数,第i+2行的第j个整数表示x[i][j]
【输出格式】
一个整数ans,表示从A到B的不经过任何坏点的路径数目
【样例输入】
2 1 2 1 1 0
【样例输出】
1
【样例解释】
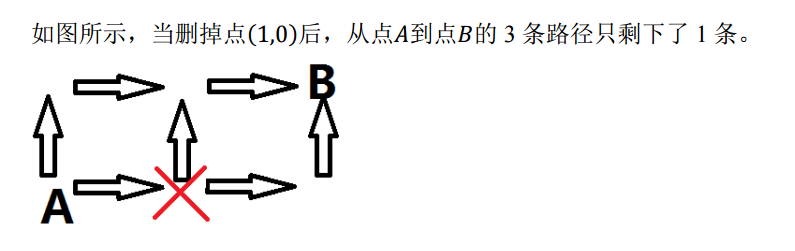
【数据范围】