| 题目名称 | 3682. 选题 |
|---|---|
| 输入输出 | mathproblem.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:8, 通过率:0% | ||||
|
|
20 | 1.815 s | 3.06 MiB | C++ |
|
|
0 | 0.004 s | 5.74 MiB | C++ |
|
|
0 | 1.030 s | 41.01 MiB | C++ |
|
|
0 | 1.034 s | 41.01 MiB | C++ |
|
|
0 | 2.366 s | 4.02 MiB | C++ |
|
|
0 | 2.377 s | 4.02 MiB | C++ |
|
|
0 | 4.690 s | 49.22 MiB | C++ |
|
|
0 | 4.694 s | 49.22 MiB | C++ |
| 本题关联比赛 | |||
| EYOI暨SBOI暑假快乐赛4th | |||
| 关于 选题 的近10条评论(全部评论) |
|---|
【题目描述】
上帝为了感谢$van$帮他修好了所有设备,派天使送给他$n$本互不相同的数学题,但$van$并不贪婪,打算拿走总共的$1/k$,也就是$n/k$个。在不同的平行宇宙中,$van$选择的$k$不相同,拿走的$n/k$本数学题也不相同,但保证$k$为$n$的正因数。这样,$van$的总方案数便是$P$。
简单来说,$P$=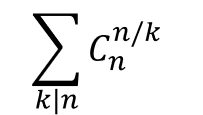 。
。
由于上帝认为$P$太大了,但不知道将$P$模一个什么数好,于是便有了$q$次询问。
对于每一次询问,上帝会在$1-m$间选择$s$个质数,第$i$个的编号$s_i$,表示从小到大数的第$s_i$个质数。上帝把它们乘起来,便得到了$Q$,接下来你需要替$van$回答:$P$%$Q$=?
【输入格式】
第一行三个正整数,$n$,$m$,$q$。
接下来$q$行,每行第一个数$s$,接下来$s$个数,第$i$个表示$s_i$。
【输出格式】
$q$行,每行一个正整数,表示答案,即$P$%$Q$。
【样例输入1】
4 5 2 1 2 2 1 3
【样例输出1】
2 1
【样例说明1】
$C_n^m$表示从$n$个不同元素中取出$m(m≤n)$个元素的所有组合的个数;
$4$的正因数有$1、2、4$,于是$P=C_4^4+C_4^2+C_4^1=1+6+4=11$。
$1$~$5$的质数有$2、3、5$。
第一次询问的$Q=3$,答案$P$%$Q=2$。
第二次询问的$Q=2*5=10$,答案$P$%$Q=1$。
【样例输入2】
12 7 4 2 1 3 2 3 4 3 1 2 4 4 1 2 3 4
【样例输出2】
8 3 38 38
【样例说明2】
$12$的正因数有$1、2、3、4、6、12$,于是:
$P=C_{12}^{12}+C_{12}^6+C_{12}^4+C_{12}^3+C_{12}^2+C_{12}^1 = 1+924+495+220+66+12=1718$,
$1$~$7$的质数有$2、3、5、7$。
第一次询问的$Q=2*5=10$,答案$P$%$Q=8$。
第二次询问的$Q=5*7=35$,答案$P$%$Q=3$。
第三次询问的$Q=2*3*7=42$,答案$P$%$Q=38$。
第四次询问的$Q=2*3*5*7=210$,答案$P$%$Q=38$。
【数据规模与约定】
对于20%的数据,$n<=20,m<=50,q<=50,Q<=100$。
对于100%的数据,$n<=10^7,m<=5×10^4,q<=10^3,Q<=5×10^7$。
【来源】
$rsr$