| 题目名称 | 2467. [HZOI 2015]完美覆盖++ |
|---|---|
| 输入输出 | coverrr.in/out |
| 难度等级 | ☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
 YGOI_真神名曰驴蛋蛋
于2016-09-17加入 |
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过：3， 提交：29， 通过率：10.34% | ||||
 1020 |
100 | 0.229 s | 22.37 MiB | C++ |
 夜雨 |
100 | 12.306 s | 1.27 MiB | C++ |
 YGOI_真神名曰驴蛋蛋 |
100 | 14.045 s | 5.38 MiB | C++ |
 poi? |
70 | 0.899 s | 2.49 MiB | C++ |
|
poi? |
70 | 13.422 s | 4.14 MiB | C++ |
|
poi? |
70 | 13.510 s | 5.12 MiB | C++ |
|
poi? |
70 | 13.547 s | 1.74 MiB | C++ |
 liuliuliu |
40 | 0.043 s | 133.73 MiB | C++ |
|
poi? |
40 | 25.526 s | 0.31 MiB | C++ |
 cuiaoxiang |
30 | 0.024 s | 0.28 MiB | C++ |
| 关于 完美覆盖++ 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
这个取模的颜色....
来自出题人的恶意啊  Hakurou!
2016-09-20 06:21
2楼
| ||||
|
递推练手题，不需要高精度
为啥我出的题目数据范围都这么鬼畜←_← YGOI_真神名曰驴蛋蛋
2016-09-18 06:09
1楼
| ||||
【题目描述】
一张普通的国际象棋棋盘，它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌，每张牌恰好覆盖棋盘上相邻的两个方格，即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么，是否能够把 32 张多米诺牌摆放到棋盘上，使得任何两张多米诺牌均不重叠，每张多米诺牌覆盖两个方格，并且棋盘上所有的方格都被覆盖住？我们把这样一种排列称为棋盘被多米诺牌完美覆盖。这是一个简单的排列问题，同学们能够很快构造出许多不同的完美覆盖。但是，计算不同的完美覆盖的总数就不是一件容易的事情了。不过，同学们 发挥自己的聪明才智，还是有可能做到的。
现在我们通过计算机编程对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。
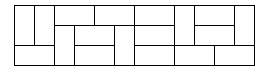
【输入格式】
一个整数N
【输出格式】
另一个整数n,表示合理方案数,答案只需对10000007取模
【样例输入】
2
【样例输出】
3
【提示】
输入文件最多达到0.1MB
【来源】
原题来自OPENJUDGE 点我传送