| 题目名称 | 3453. 电影票的密码 |
|---|---|
| 输入输出 | PhD.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 233 MiB |
| 测试数据 | 5 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:5, 提交:8, 通过率:62.5% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.015 s | 3.51 MiB | C++ |
|
|
0 | 0.000 s | 0.00 MiB | C++ |
|
|
0 | 0.002 s | 13.66 MiB | C++ |
|
|
0 | 0.003 s | 6.74 MiB | C++ |
| 关于 电影票的密码 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
题解已在题目下面贴出来,个人推荐法1
其实我们需要用到的只有斐波那契数列的前两项,所以无论这个f数列是什么,f2及以后的都是无用数列。 关键在推导出这个 $$ \sum_{i}^{+∞} a_i = \sum_{i-1}^{+∞}\frac {a_{i-1} }{K} + \sum_{i-2}^{+∞}\frac {a_{i-2} }{K^2} $$ 只要推出来了就很容易得出下面这些 $$ S-a_0-a_1 = S - \frac {a_0}{K} + \frac {S}{K^2}$$ $$ S= S-\frac {a_0}{K} + \frac {S}{K^2} +a_0 + a_1 $$ $$ S -\frac {S}{K} -\frac {S}{K^2}= \frac {-a_0}{K} + a_0 + a_1 = \frac {-1}{K}+1+\frac {1}{K}=1 $$ $$ S = \frac {1}{1-\frac {1}{K}-\frac {1}{K^2}}$$ 比较容易看懂 法2的话理解limit也可以试试看,不过忽略了前期简单推导,和法1差不多
2021-07-02 16:28
2楼
| ||||
|
(或许没bug的)题解剧透注意
本题思路1:  事实证明应该没有bug,但是居然会收敛 思路2: 
2021-07-02 11:21
1楼
| ||||
ps:欢迎来找bug
【题目描述】
Fello是一个奆佬,他平时喜欢去电影院看新上映的电影,而且每部电影绝不缺席。有一天新上映了一部电影《Promare》,Fello非常喜欢这部电影,所以他想去抢电影票。店家的抢票政策非常有意思:抢购电影票需要输入密码,设想买这部电影票的有K人(k≥2),则抢购电影票的密码为:
$$ S = \sum_{i=0}^{+∞} \frac {f_i}{K^i}$$
其中f序列的值没人知道,店家给出了f序列的前五位:$${f[0]=1,f[1]=1,f[2]=2,f[3]=3,f[4]=5}。$$
由于这实在是一部绝世的好电影,Fello非常想看,请你帮帮他求出电影票的密码。
【输入格式】
一个正整数K(1000≥K≥2)
【输出格式】
输出抢购电影票的密码,保留小数点后第四位。
【样例输入】
5
【样例输出】
1.3158
【提示】
答案剧透注意!
——————————
本题目更倾向于数学推导。部分过程如下:(手打要累死了。。)
$$ 设\frac{f_i}{K^i} = a_i .经过一系列推算可以得出 $$
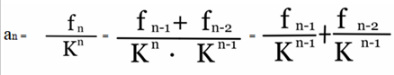
$$ \sum_{i}^{+∞} a_i = \sum_{i-1}^{+∞}\frac {a_{i-1} }{K} + \sum_{i-2}^{+∞}\frac {a_{i-2} }{K^2} $$
不妨先求
$$ S-a_0-a_1 = S - \frac {a_0}{K} + \frac {S}{K^2}$$
然后等号左右两边相应移位可以得出
$$ S= S-\frac {a_0}{K} + \frac {S}{K^2} +a_0 + a_1 $$
易得
$$ S -\frac {S}{K} -\frac {S}{K^2}= \frac {-a_0}{K} + a_0 + a_1 = \frac {-1}{K}+1+\frac {1}{K}=1 $$
这样就可以知道
$$ S = \frac {1}{1-\frac {1}{K}-\frac {1}{K^2}}$$
或者,有一个简单的思路。
$$ 当n→+∞时,可以知道\frac {f{n-1}}{K^n}=\frac {f_n}{K^{n+1}} = 0.本题目所求可以从 $$
$$ S_n = \frac {\frac {f_{n+1}}{K^n} - K + \frac {f_n}{K^{n+1}}}{1+\frac {1}{K}-K} $$
变为
$$ S = \frac {-K}{1+\frac {1}{K}-K}$$
然后就可以得出
$$ S = \frac {1}{1-\frac {1}{K}-\frac {1}{K^2}}$$