| 题目名称 | 1171. 树的重量 |
|---|---|
| 输入输出 | treeweight.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 1 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:6, 提交:14, 通过率:42.86% | ||||
|
|
100 | 0.001 s | 0.30 MiB | C++ |
|
|
100 | 0.001 s | 4.14 MiB | C++ |
|
|
100 | 0.002 s | 0.30 MiB | C++ |
|
|
100 | 0.003 s | 0.32 MiB | C++ |
|
|
100 | 0.004 s | 0.36 MiB | C++ |
|
|
100 | 0.007 s | 0.00 MiB | Pascal |
|
|
0 | 0.000 s | 0.17 MiB | Pascal |
|
|
0 | 0.001 s | 0.36 MiB | C++ |
|
|
0 | 0.002 s | 0.36 MiB | C++ |
|
|
0 | 0.004 s | 0.21 MiB | Pascal |
| 关于 树的重量 的近10条评论(全部评论) |
|---|
【问题描述】
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j]+M[j,k]<=M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
如下图,矩阵M描述了一棵树。
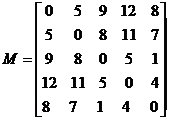
树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。
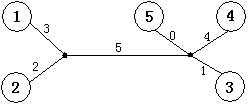
【输入】
输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-l行,给出的是矩阵M的一个上三角(不包含对角线),矩阵中所有元素是不超过100的非负整数。输入数据保证合法。
输入数据以n=0结尾。
【输出】
对于每组输入,输出一行,一个整数,表示树的重量。
【样例】
weight.in weight.out
5 15
5 9 12 8 71
8 11 7
5 1
4
4
15 36 60
31 55
36
0